题目内容
13.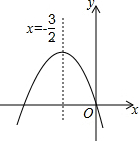 如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac-b2<0.其中正确结论有①③④.
分析 首先根据二次函数y=ax2+bx+c的图象经过原点,可得c=0,所以abc=0;然后根据x=1时,y<0,可得a+b+c<0;再根据图象开口向下,可得a<0,图象的对称轴为x=-$\frac{b}{2a}$=-$\frac{3}{2}$,所以b=3a,a>b;最后根据二次函数y=ax2+bx+c图象与x轴有两个交点,可得△>0,所以b2-4ac>0,4ac-b2<0,据此解答即可.
解答 解:∵二次函数y=ax2+bx+c图象经过原点,
∴c=0,
∴abc=0,故①正确;
∵x=1时,y<0,
∴a+b+c<0,故②不正确;
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴是x=-$\frac{3}{2}$,
∴-$\frac{b}{2a}$=-$\frac{3}{2}$,
∴b=3a,
又∵a<0,b<0,
∴a>b,故③正确;
∵二次函数y=ax2+bx+c图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,4ac-b2<0,故④正确;
综上,可得正确结论有3个:①③④.
故答案为①③④.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
4.我市一水果销售公司,需将一批鲜桃运往某地,有汽车、火军两种运输工具可供选择,两种运输工具的主要参考数据如下:
假设这批水果在运输过程中(含装卸时间)的损耗为160元/时.
(1)当运输路程为400千米时,你认为采用哪种运输工具比较好?
(2)当运输路程为多少千米时,两种运输工具所需总费用相同.
| 运输工具 | 途中平均费用(单位:元/千米) | 途中平均速度(单位:千米/时) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
| 汽车 | 10 | 80 | 2 | 1000 |
| 火车 | 8 | 100 | 4 | 2000 |
(1)当运输路程为400千米时,你认为采用哪种运输工具比较好?
(2)当运输路程为多少千米时,两种运输工具所需总费用相同.
2.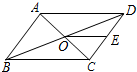 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
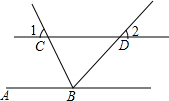 如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.
如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.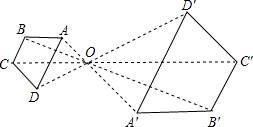 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.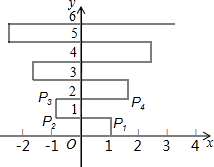 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是(2,2),点P第8次跳动至P8的坐标为(3,4);则点P第256次跳动至P256的坐标是(65,128).