题目内容
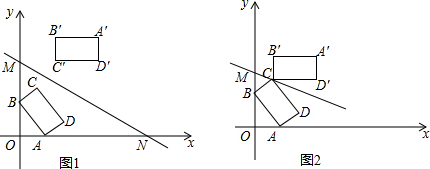
17.如图1,矩形ABCD的顶点A(6,0),B(0,8),AB=2BC,直线y=-$\frac{1}{2}$x+m(m≥13)交坐标轴于M,N两点,将矩形ABCD沿直线y=-$\frac{1}{2}$x+m(m≥13)翻折后得到矩形A′B′C′D′.(1)求点C的坐标和tan∠OMN的值;
(2)如图2,直线y=-$\frac{1}{2}$x+m过点C,求证:四边形BMB′C是菱形;
(3)如图1,在直线y=-$\frac{1}{2}$x+m(m≥13)平移的过程中.
①求证:B′C′∥y轴;
②若矩形A′B′C′D′的边与直线y=-x+43有交点,求m的取值范围.
分析 (1)首先利用勾股定理求得AB的长,然后证明△AOB∽△BEC,根据相似三角形的对应边的比相等求得BE的长,则OE长即可求得,从而求得C的坐标;
(2)利用待定系数法求得m的值,求得BM的长,根据四边相等的四边形是菱形即可证得;
(3)①如图3,连接BB′,同理若延长B'C'和BC交于点I,则I在MN上,过C作EQ∥MN,作出CB关于EQ的对称线段CG,则EQ就是(2)中的MN,证明B'C'∥CG即可;
②过B′作B′F⊥y轴于点F,设B′F=a,则BF=2a,设BM=B′M=b,则MF=2a-b,在直角△B′FM中利用勾股定理求得a和b的比值,MF和B′F即可利用m表示出来,A′和C′坐标即可求得,代入直线y=-x+43求得m的值,从而确定m的范围.
解答 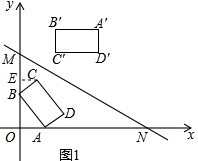 解:(1)∵A(6,0),B(0,8).
解:(1)∵A(6,0),B(0,8).
∴OA=6,OB=8,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴BC=$\frac{1}{2}$AB=5.
如图1,过C作CE⊥y轴于点E,
∴∠BOA=∠CEB=90°,
又∵∠BAO+∠ABO=∠EBC+∠ABO=90°,
∴∠BAO=∠EBC,
∴△AOB∽△BEC,
∴$\frac{AO}{BE}$=$\frac{BO}{EC}$=$\frac{AB}{BC}$=2,
∴BE=3,CE=4.
∴OE=BE-OB=11,
∴点C的坐标是(4,11).
当x=0时,OM=m,当y=0时,ON=2m,
∴tan∠OMN=2;
(2)如图2,由题意得:BM=B'M,BC=B′C.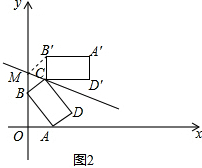
∵直线y=-$\frac{1}{2}$x+m过点C(4,11).
∴11=-2+m,
解得:m=13,
∴BM=13-8=5,
∴B'M=BM=BC=B'C=5,
∴四边形BMB′C是菱形;
(3)①如图3,连接BB′,同理若延长B'C'和BC交于点I,则I在MN上,
过C作EQ∥MN,作出CB关于EQ的对称线段CG,
则EQ就是(2)中的MN.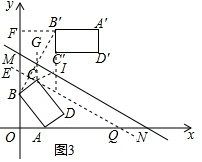
根据(2)可得CG∥BM,且∠BCE=∠MCG,
∵MN∥EQ,
∴∠BCE=∠CIM,
又∵∠CIM=∠MIB',
∴∠BCG=∠CIB',
∴B'C'∥BM,
即B′C′∥y轴.
②如图3,过B′作B′F⊥y轴于点F.
∵BB′⊥MN,
∴tan∠MBB′=$\frac{1}{2}$,
∴BF=2B′F,
设B′F=a,则BF=2a,设BM=B′M=b,则MF=2a-b,
在直角△B′FM中,a2+(2a-b)2=b2,
解得:a:b=4:5.
∴MF:B′F:B′M=3:4:5.
∵B′M=BM=m-8,
∴MF=$\frac{3}{5}$(m-8),B′F=$\frac{4}{5}$(m-8).
则OF=OB+BF=8+2a=8+2B'F=8+2×$\frac{4}{5}(m-8)$=$\frac{8m-24}{5}$,
A'F=B’F+A'B'=$\frac{4}{5}(m-8)$+10=$\frac{4m+18}{5}$,
∴A′坐标是($\frac{4m+18}{5}$,$\frac{8m-24}{5}$),
C'的纵坐标是OF-B'C'=$\frac{8m-24}{5}$-5=$\frac{8m-49}{5}$,
则C′的坐标是:($\frac{4m-32}{5}$,$\frac{8m-49}{5}$),
当点A′在直线y=-x+43上时,m=$\frac{221}{12}$,
当点C′在直线y=-x+43上时,m=$\frac{74}{3}$.
∴则m的取值范围是$\frac{221}{12}$≤m≤$\frac{74}{3}$.
点评 本题考查了一次函数与相似三角形的判定与性质的综合应用,正确利用m表示出B′和C′坐标是解决本题的关键.

 如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )
如图,在7×7的正方形网格中,每个小正方形的边长为1,画一条线段AB=$\sqrt{50}$,使点A,B在小正方形的顶点上,设AB与网格线相交所成的锐角为α,则不同角度的α有( )| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
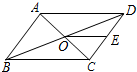 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
| A. | -4a2 | B. | 2a2 | C. | 4a | D. | 4a2 |
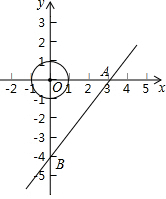 如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,-4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是$\frac{7}{4}$<t<$\frac{17}{4}$.
如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,-4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是$\frac{7}{4}$<t<$\frac{17}{4}$.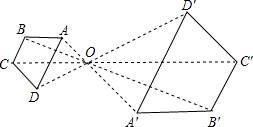 如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.
如图,以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′,若OA=4,OA′=8,则四边形ABCD和四边形A′B′C′D′的周长的比为1:2.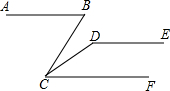 如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.
如图,AB∥DE,∠ABC=70°,∠CDE=130°,∠BCF=70°.