题目内容
12. 如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.
如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.(1)求证:四边形ABDE是等腰梯形;
(2)若EC=2,BE=1,∠AOD=2∠1,求AB的长.
分析 (1)由等腰三角形的性质得出∠CDE=∠CED,由三角形的外角性质和已知条件得出∠AED=∠BDE,证出OD=OE,由AAS证明△AOD≌△BOE,得出AD=BE,OA=OB,由等腰三角形的性质得出∠OAB=∠OBA,再由对顶角相等和三角形内角和定理得出∠OAB=∠OBA=∠ODE=∠OED,证出DE∥AB,即可得出结论;
(2)由三角形的外角性质和已知条件得出∠1=∠OED,证出AD=ED=BE=1,由平行线的性质得出△CDE∽△CAB,得出对应边成比例,即可得出AB的长.
解答 (1)证明:∵CD=CE,
∴∠CDE=∠CED,
∵∠CDE=∠2+∠AED,∠CED=∠1+∠BDE,∠1=∠2,
∴∠AED=∠BDE,
∴OD=OE,
在△AOD和△BOE中,
$\left\{\begin{array}{l}{∠2=∠1}&{\;}\\{∠AOD=∠BOE}&{\;}\\{OD=OE}&{\;}\end{array}\right.$,
∴△AOD≌△BOE(AAS),
∴AD=BE,OA=OB,
∴∠OAB=∠OBA,
∵∠AOD=∠BOE,
∴∠OAB=∠OBA=∠ODE=∠OED,
∴DE∥AB,
∴四边形ABDE是等腰梯形;
(2)解:∵∠AOD=2∠1=∠ODE+∠OED,∠OED=∠ODE,
∴∠1=∠OED,
∴AD=ED=BE=1,
∵DE∥AB,
∴△CDE∽△CAB,
∴$\frac{DE}{AB}=\frac{EC}{BC}$,
即$\frac{1}{AB}=\frac{2}{1+2}$,
解得:AB=$\frac{3}{2}$.
点评 本题考查了等腰梯形的判定、等腰三角形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质等知识;熟练掌握等腰梯形的判定,证明三角形全等和三角形相似是解决问题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 正数、负数统称为有理数 | B. | 无限小数都是无理数 | ||
| C. | 有理数、无理数统称为实数 | D. | 两个无理数的和一定是无理数 |
| 运输工具 | 途中平均费用(单位:元/千米) | 途中平均速度(单位:千米/时) | 装卸时间(单位:小时) | 装卸费用(单位:元) |
| 汽车 | 10 | 80 | 2 | 1000 |
| 火车 | 8 | 100 | 4 | 2000 |
(1)当运输路程为400千米时,你认为采用哪种运输工具比较好?
(2)当运输路程为多少千米时,两种运输工具所需总费用相同.
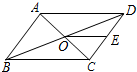 如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )
如图,?ABCD的周长为28,对角线AC、BD相交于点O.点E是CD的中点,BD=10,则△DOE的周长为( )| A. | 28 | B. | 24 | C. | 12 | D. | 17 |
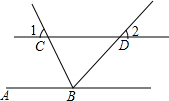 如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.
如图,直线AB∥CD,BC平分∠ABD,∠1=67°,则∠2=46度.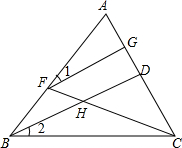 如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.
如图,已知BD平分∠ABC,点F在AB上,点G在AC上,连接FG、FC,FC与BD相交于点H,如果∠GFH与∠BHC互补.求证:∠1=∠2.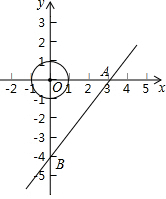 如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,-4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是$\frac{7}{4}$<t<$\frac{17}{4}$.
如图,在直角坐标系中,直线AB交x轴、y轴于点A(3,0)与B(0,-4),现有一半径为1的动圆的圆心位于原点处,动圆以每秒1个单位长度的速度向右作平移运动.设运动时间为t(秒),则动圆与直线AB相交时t的取值范围是$\frac{7}{4}$<t<$\frac{17}{4}$.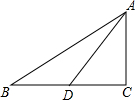 如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.