题目内容
20.计算:(1)$\frac{2x}{x-y}+\frac{2y}{y-x}$
(2)$({\frac{a+2}{{{a^2}-2a}}-\frac{a-1}{{{a^2}-4a+4}}})÷\frac{4-a}{{{a^2}-2a}}$.
分析 (1)根据同分母分式相加减进行计算即可;
(2)先算括号内的式子,能分解因式的先分解因式,然后通分再根据有理数的除法法则进行计算即可.
解答 解:(1)$\frac{2x}{x-y}+\frac{2y}{y-x}$
=$\frac{2x}{x-y}-\frac{2y}{x-y}$
=$\frac{2x-2y}{x-y}$
=$\frac{2(x-y)}{x-y}$
=2;
(2)$({\frac{a+2}{{{a^2}-2a}}-\frac{a-1}{{{a^2}-4a+4}}})÷\frac{4-a}{{{a^2}-2a}}$
=$[\frac{a+2}{a(a-2)}-\frac{a-1}{(a-2)^{2}}]×\frac{a(a-2)}{4-a}$
=$\frac{(a+2)(a-2)-a(a-1)}{a(a-2)^{2}}×\frac{a(a-2)}{4-a}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{a(a-2)^{2}}×\frac{a(a-2)}{4-a}$
=$\frac{a-4}{a(a-2)^{2}}×\frac{a(a-2)}{4-a}$
=$\frac{-1}{a-2}$.
点评 本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算方法.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
11.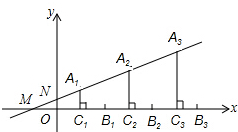 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
8.点P(-2,1)关于x轴的对称点所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.方程2x2-ax+7=0,有一根是$\frac{1}{2}$,则另一根为( )
| A. | 7 | B. | 7.5 | C. | -7 | D. | 15 |
12.2014年1月,Rain时隔四年,发布他第六张专辑《Rain Effect》,Rain为宣传专辑频繁赶通告,Rain所在的公司原计划在2月要Rain出席30个通告,后因新专辑反映热烈,在2月又增加了15个通告,并且比原计划多出席了5天的通告.已知Rain每天出席通告的个数与原计划的相同,求Rain原计划要出席多少天的通告?设Rain原计划要出席x天的通告,根据题意可列正确的方程是( )
| A. | $\frac{30}{x}=\frac{30+15}{x+5}$ | B. | $\frac{30}{x}=\frac{30+15}{x}+5$ | C. | $\frac{30}{x}+5=\frac{30+15}{x}$ | D. | $\frac{30}{x+5}=\frac{30+15}{x}$ |
 如图,AB是⊙O的直径,弦CD与AB相交于点E.
如图,AB是⊙O的直径,弦CD与AB相交于点E.
 近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?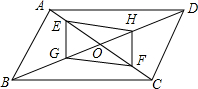 如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.
如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.求证:四边形EGFH是平行四边形.