题目内容
10．
如图，AB是⊙O的直径，弦CD与AB相交于点E．（1）若∠CAB=65°，求∠D的度数；
（2）若AE=10，EB=2，且∠AEC=30°，求CD的长．
分析 （1）连接BC，由AB是⊙O的直径，得到∠ACB=90°，根据圆周角定理即可得到结论；
（2）因为∠AEC=30°，可过点O作OF⊥CD于F，构成直角三角形，先求得⊙O的半径为5cm，进而求得OE=4，根据30°角所对的直角边等于斜边的一半，得出OF=$\frac{1}{2}$OE=2，再根据勾股定理求得DF的长，然后由垂径定理求出CD的长．
解答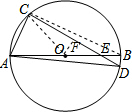 
解：（1）连接BC，
∵AB是⊙O的直径，
∴∠ACB=90°，
∵∠CAB=65°，
∴∠B=25°，
∴∠D=∠B=25°；
（2）连接OC，过点O作OF⊥CD于点F；
∵AE=10，BE=2，
∴OC=OA=6，OE=6-2=4；
∵∠AEC=30°，
∴OF=2，
由勾股定理得：CF2=OC2-OF2，
解得：CF=$\sqrt{21}$，
∴CD=2CF=2$\sqrt{21}$．
点评 该题主要考查了垂径定理、勾股定理等几何知识点及其应用问题；解题的方法是作辅助线，构造直角三角形；解题的关键是灵活运用垂径垂径定理、勾股定理等几何知识点来分析、判断、解答．
练习册系列答案
相关题目
如图，一个长方形的长减去4cm，宽增加2cm，就成为一个正方形，并且这两个图形的面积相等，这个长方形的长、宽各是多少？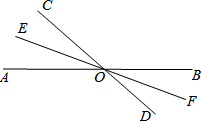
如图所示，已知直线AB、CD相交于点O，OE、OF分别是∠AOC、∠BOD的角平分线，射线OE、OF在同一条直线上吗？为什么？
如图，在△ABC中，∠ACB=90°，∠ABC=60°，BD平分∠ABC，P点是BD的中点，若AD=6，则CP的长为3．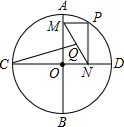
如图，⊙O的半径为2，AB，CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A，B，C，D不重合），过点P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为$\frac{π}{4}$．
15．下列命题正确的是（ ）
| A． | 若两条弧的长相等，则这两条弧是等弧 | |
| B． | 两条弧的长相等，它们所对的圆心角也相等 | |
| C． | 两个相等的圆心角所对的两条弧的长相等 | |
| D． | 如果两个圆的周长相等，那么它们的半径也相等 |
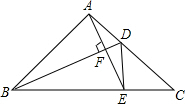如图，在△ABC中，BD是角平分线，AB=AC=5，BC=8，过A作AE⊥BD交于F，交BC于E，连结DE，则S△ABF：S△CDE=$\frac{65}{48}$．