题目内容
11.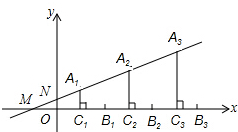 如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )
如图,直线y=$\frac{1}{2}$x+1分别与x轴、y轴交于点M,N,一组线段A1C1,A2C2,A3C3,…AnCn的端点A1,A2,A3,…An依次是直线MN上的点,这组线段分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,若OB1=B1B2=B2B3=…=Bn-1Bn=4,则点An到x轴的距离为( )| A. | 4n-4 | B. | 4n-2 | C. | 2n | D. | 2n-2 |
分析 由直线解析式可以找出M、N点坐标,即得出NO、MO的长度,再由已知得出OC1,OC2,OC3,…,OCn这组线段的长度,依据三角形相似的性质可得出结论.
解答 解:令x=0,则有y=1;
令y=0,则有$\frac{1}{2}$x+1=0,解得:x=-2.
故点M(-2,0),点N(0,1).
∵一组线段A1C1,A2C2,A3C3,…AnCn分别垂直平分线段OB1,B1B2,B2,B3,…,Bn-1Bn,且OB1=B1B2=B2B3=…=Bn-1Bn=4,
∴OC1=2,OC2=4+2,OC3=4×2+2,…,OCn=4×(n-1)+2,
∴MC1=4,MC2=4+4,MC3=4×2+4,…,MCn=4×(n-1)+4=4n.
∵AnCn∥y轴,
∴△MNO∽△MAnCn,
∴$\frac{{A}_{n}{C}_{n}}{NO}$=$\frac{M{C}_{n}}{MO}$.
∵NO=1,MO=2,
∴AnCn=MCn•$\frac{NO}{MO}$=2n.
故选C.
点评 本题考查了坐标系上点的特征依据相似三角形的判定及性质,解题的关键是找出OC1,OC2,OC3,…,OCn这组线段的长度.本题属于基础题,难度不大,解决该类问题的技巧是选找到线段长度的规律.

练习册系列答案
相关题目
6.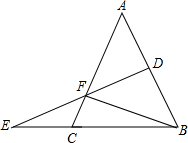 如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )
如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )
 如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )
如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,则△BCF的周长和∠EFC分别等于( )| A. | 16,40° | B. | 8,50° | C. | 16,50° | D. | 8,40° |
16.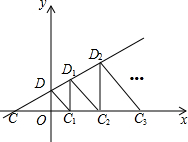 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
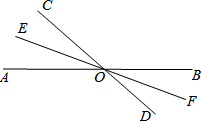 如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?
如图所示,已知直线AB、CD相交于点O,OE、OF分别是∠AOC、∠BOD的角平分线,射线OE、OF在同一条直线上吗?为什么?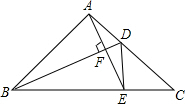 如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.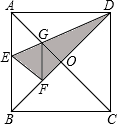 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论: