题目内容
9. 近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
近年来,合肥“大建设”已经取得了令人瞩目的成就,今年合肥市继续重点实施综合交通、园林绿化和环境综合整治等八大类工程.如图是某建筑工地搭建的临时帐篷的横截面,其上下轮廓线分别由抛物线对称的一部分和矩形的一部分构成,最大高度为6米,底部宽度为12米,OE=3米,如果还要搭建一个矩形“支撑架”,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长L(L=AD+DC+CB)的最大值是多少?
分析 由图可得M,P的坐标,易求出这条抛物线的函数解析式.设A(m,0),则B(12-m,0),C(12-m,-$\frac{1}{12}$m2+m+3),D(m,-$\frac{1}{12}$m2+m+3),根据支撑架”总长L=AD+DC+CB列出关于m的函数关系式,可得最大值.
解答 解:如图,以O点为原点,OM所在直线为x轴建立直角坐标系.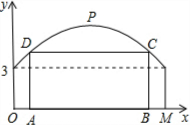
由题意得:M(12,0),P(6,6),
由顶点P(6,6),设此函数解析式为:y=a(x-6)2+6,
将点(0,3)代入得a=-$\frac{1}{12}$,
∴y=-$\frac{1}{12}$(x-6)2+6
=-$\frac{1}{12}$x2+x+3;
设A(m,0),则B(12-m,0),C(12-m,-$\frac{1}{12}$m2+m+3),D(m,-$\frac{1}{12}$m2+m+3)
∴“支撑架”总长AD+DC+CB=(-$\frac{1}{12}$m2+m+3)+(12-2m)+(-$\frac{1}{12}$m2+m+3)=-$\frac{1}{6}$m2+18,
∵此二次函数的图象开口向下.
∴当m=0时,AD+DC+CB有最大值为18.
点评 本题主要考查二次函数的应用能力,建立合适坐标系求解析式是解决问题的根本,求二次函数的最大(小)值是关键,通常有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
相关题目
4.某校安排三辆车,组织八年级学生参加“合肥工业游”活动,其中方圆与吴敏同学都可以从这三辆车中任选一辆搭乘,则方圆与吴敏同车的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
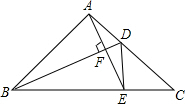 如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
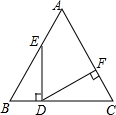 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.
如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.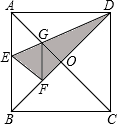 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB、AC于点E、G.连接GF,下列结论: