题目内容
5.如图1,点P是∠MON平分线上的点,射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON于点B,且使∠APB+∠MON=180°.(1)求证:PA=PB;
(2)如图2,若∠MON=60°,OB=2,射线AP交ON于点D,且满足∠PBD=∠ABO,求OP的长.

分析 (1)作PE⊥OM,PF⊥ON,垂足为M、N,由四边形内角和定理可知∠EPF+∠MON=180°,已知∠APB+∠MON=180°,则∠EPF=∠APB,可证∠EPA=∠FPB,由角平分线的性质,得PE=PF,可证△EPA≌△FPB,得出结论;
(2)作BH⊥OT,垂足为T,当∠MON=60°时,∠APB=120°,由PA=PB得∠PBA=∠PAB=30°,又∠PBD=∠ABO,∠PBD+∠PBA+∠ABO=180°,可求∠ABO度数为75°,从而∠OBP=105°,在△OBP中,∠BOP=30°,则∠BPO=45°,分别解Rt△OBH,Rt△PBH即可求OP.
解答 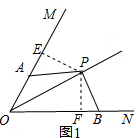 解:(1)作PE⊥OM,PF⊥ON,垂足为E、F
解:(1)作PE⊥OM,PF⊥ON,垂足为E、F
∵四边形OEPF中,∠OEP=∠OFP=90°,
∴∠EPF+∠MON=180°,已知∠APB+∠MON=180°,
∴∠EPF=∠APB,即∠EPA+∠APF=∠APF+∠FPB,
∴∠EPA=∠FPB,
由角平分线的性质,得PE=PF,
在△EPA与△FPB中,
$\left\{\begin{array}{l}{∠OEP=∠OFP}\\{PE=PF}\\{∠EPA=∠FPB}\end{array}\right.$,
∴△EPA≌△FPB,
∴PA=PB;
(2)作BH⊥OP,垂足为H,
当∠MON=60°时,∠APB=120°,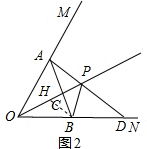
由PA=PB,得∠PBA=∠PAB=$\frac{1}{2}$(180°-∠APB)=30°,
又∵∠PBD=∠ABO,∠PBD+∠PBA+∠ABO=180°,
∴∠ABO=$\frac{1}{2}$(180°-30°)=75°,则∠OBP=∠ABO+∠ABP=105°,
在△OBP中,∵∠BOP=30°,
∴∠BPO=45°,
在Rt△OBH中,BH=$\frac{1}{2}$OB=1,OH=$\sqrt{3}$,
在Rt△PBH中,PH=BH=1,
∴OP=OH+PH=$\sqrt{3}$+1.
点评 本题考查了全等三角形的判定和性质,旋转的性质的运用.正确作出辅助线是解题的关键.

| A. | 若两条弧的长相等,则这两条弧是等弧 | |
| B. | 两条弧的长相等,它们所对的圆心角也相等 | |
| C. | 两个相等的圆心角所对的两条弧的长相等 | |
| D. | 如果两个圆的周长相等,那么它们的半径也相等 |
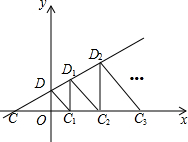 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
| A. | 调查某总学全体学生的身体素质情况 | |
| B. | 调查某市中学生压岁钱的使用情况 | |
| C. | 调查某班全体学生的身高 | |
| D. | 调查某品牌烟花爆竹燃放安全的情况 |




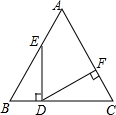 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.
如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.