题目内容
任意掷一枚质地均匀的骰子,朝上的点数是奇数的概率是______.
 【解析】任意掷一枚质地均匀的骰子,朝上的点数可能是1,2,3,4,5,6,其中有三个奇数,因此朝上的点数是奇数的概率是.故答案为: .
【解析】任意掷一枚质地均匀的骰子,朝上的点数可能是1,2,3,4,5,6,其中有三个奇数,因此朝上的点数是奇数的概率是.故答案为: .
练习册系列答案
相关题目
当x=-2时,代数式ax3+bx+1的值是2 017,那么当x=2时,代数式ax3+bx+1的值是____.
 -2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015.
-2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015. 某种零件规格是 mm,下列尺寸的该种零件,不合格的是( )
mm,下列尺寸的该种零件,不合格的是( )
A. 19.7 mm B. 19.8 mm C. 20 mm D. 20.05 mm
 A
【解析】试题分析:mm的范围为19.8mm<零件合格尺寸<20.2mm。所以不合格的是A。
A
【解析】试题分析:mm的范围为19.8mm<零件合格尺寸<20.2mm。所以不合格的是A。 已知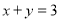 ,
, 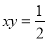 ,则多项式
,则多项式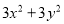 的值为( ).
的值为( ).
A. 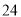 B.
B. 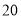 C.
C. 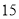 D.
D. 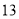
 A
【解析】试题解析:∵x+y=3,
故选A.
A
【解析】试题解析:∵x+y=3,
故选A. 用10个球设计一个摸球游戏:
(1)使摸到红球的概率为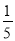 ;
;
(2)使摸到红球和白球的概率都是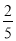 .
.
 (1)2个红球,8个白球;(2)4个红球,4个白球,2个其他颜色球.
【解析】分析:本题考察对概率意义的理解,关键是根据要求,算出符合条件的各色小球的个数.
本题解析:
(1)在一个不透明的口袋内装大小材质相同的小球,其中2个红球,8个为白球,则摸到红球的概率符合要求.
(2)在一个不透明的口袋内装大小材质相同的小球,其中4个红球,4个白球,2个黑球,则摸到红球和白球的的概...
(1)2个红球,8个白球;(2)4个红球,4个白球,2个其他颜色球.
【解析】分析:本题考察对概率意义的理解,关键是根据要求,算出符合条件的各色小球的个数.
本题解析:
(1)在一个不透明的口袋内装大小材质相同的小球,其中2个红球,8个为白球,则摸到红球的概率符合要求.
(2)在一个不透明的口袋内装大小材质相同的小球,其中4个红球,4个白球,2个黑球,则摸到红球和白球的的概... 甲乙两人做游戏,同时掷两枚相同的硬币,双方约定:同面朝上甲胜,异面朝上则乙胜,则这个游戏对双方( )
A. 公平 B. 对甲有利 C. 对乙有利 D. 无法确定公平性
 A
【解析】解析:同时掷两枚相同的硬币,所有等可能的事件如下表所示:
硬币
朝上的面
朝上的面
朝上的面
朝上的面
硬币一
国徽
国徽
数字
数字
硬币二
国徽
数字
国徽
数字
是否同面
同面
异面
同面
异面
同面朝上的概率为,异面朝上的概率为,故选A.
...
A
【解析】解析:同时掷两枚相同的硬币,所有等可能的事件如下表所示:
硬币
朝上的面
朝上的面
朝上的面
朝上的面
硬币一
国徽
国徽
数字
数字
硬币二
国徽
数字
国徽
数字
是否同面
同面
异面
同面
异面
同面朝上的概率为,异面朝上的概率为,故选A.
... 小刚掷一枚硬币,一连9次都掷出正面朝上,当他第十次掷硬币时,出现正面朝上的概率是( )
A. 0 B. 1 C. 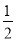 D.
D. 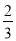
 C
【解析】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C.
C
【解析】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C. 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
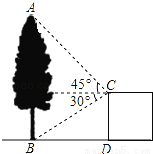
 5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m.
5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m. 三角形的一个外角是锐角,则此三角形的形状是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 无法确定
 B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。
B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。 
