题目内容
在△ABC中,∠A=105°,∠B=45°,cosC的值是( )
A.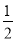 B.
B.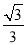 C.
C.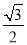 D.
D.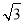
 C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.
C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.
练习册系列答案
相关题目
某种零件规格是 mm,下列尺寸的该种零件,不合格的是( )
mm,下列尺寸的该种零件,不合格的是( )
A. 19.7 mm B. 19.8 mm C. 20 mm D. 20.05 mm
 A
【解析】试题分析:mm的范围为19.8mm<零件合格尺寸<20.2mm。所以不合格的是A。
A
【解析】试题分析:mm的范围为19.8mm<零件合格尺寸<20.2mm。所以不合格的是A。 小刚掷一枚硬币,一连9次都掷出正面朝上,当他第十次掷硬币时,出现正面朝上的概率是( )
A. 0 B. 1 C. 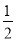 D.
D. 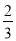
 C
【解析】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C.
C
【解析】小刚掷一枚硬币,他第十次掷硬币,出现正面朝上还是反而朝上,与前面九次没有任何联系,这十次掷硬币,是十个相互独立的事件,每一次正面朝上与反面朝上,都是概率相同的.故选C. 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
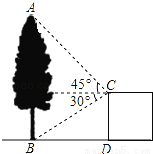
 5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m.
5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
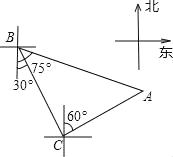
AB=BE+AE=(5+5)m. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A.25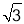 B.25
B.25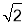 C.50 D.25
C.50 D.25
 D.
【解析】
试题分析:根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.如图:根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故选D.
D.
【解析】
试题分析:根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.如图:根据题意,∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故选D. 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
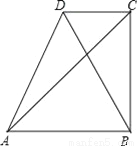
 6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm.
6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm. 把一副常用的三角形如图所示拼在一起,那么图中∠ADE是__度.
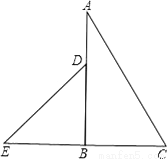
 135°
【解析】试题分析:根据三角板可得:∠BDE=45°,则根据平角的性质可得:∠ADE=180°-45°=135°.
135°
【解析】试题分析:根据三角板可得:∠BDE=45°,则根据平角的性质可得:∠ADE=180°-45°=135°. 三角形的一个外角是锐角,则此三角形的形状是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 无法确定
 B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。
B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。 抛掷一枚质地均匀的硬币,落地后正面朝上的概率是 .
 .
【解析】
试题分析:抛掷一枚质地均匀的硬币,等可能的情况有:正面朝上,反面朝上,则P(正面朝上)=,故答案为:.
.
【解析】
试题分析:抛掷一枚质地均匀的硬币,等可能的情况有:正面朝上,反面朝上,则P(正面朝上)=,故答案为:. 
