题目内容
18.已知一次函数y=kx+b的图象经过点(2,3),与y轴交于点B(0,4),与x轴交于点A.(1)求一次函数的解析式;
(2)求方程kx+b=0的解;
(3)求该函数图象与两坐标轴围成三角形的面积.
分析 (1)把(2,3),与y轴交于点B(0,4)分别代入y=kx+b得到关于k、b的方程组,然后解方程组求出k、b即可得到一次函数解析式;
(2)求(1)中的一次函数的函数值为0时的自变量的值可得到方程kx+b=0的解;
(3)先由(2)可得A点坐标,然后根据三角形面积公式求解.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{2k+b=3}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
所以一次函数解析式为y=-$\frac{1}{2}$x+4;
(2)当y=0时,-$\frac{1}{2}$x+4=0,解得x=8;
(3)由(2)得一次函数与x轴的交点A的坐标为(8,0),
所以该函数图象与两坐标轴围成三角形的面积=$\frac{1}{2}$×4×8=16.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: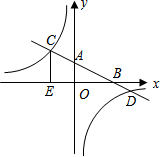 如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,已知一次函数y=kx+b的图象分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.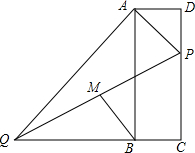 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.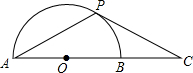 如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA
如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA 如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.
如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.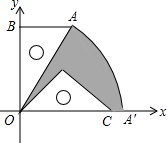 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)