题目内容
6.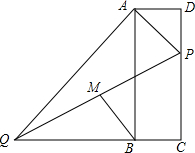 如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,当DP=8时,求线段BM的长.
分析 (1)根据矩形的性质得出∠D=∠ABC=90°,∠DAB=90°,求出∠QAB=∠DAP,∠ABQ=∠D,根据相似三角形的判定得出即可;
(2)作MN⊥QC,根据相似三角形的判定得出△MQN∽△PQC,根据相似三角形的性质得出$\frac{MN}{PC}=\frac{QM}{QP}$,根据已知条件得到$\frac{MN}{PC}=\frac{1}{2}$,求得MN=$\frac{1}{2}$PC=$\frac{1}{2}$(20-8)=6,QN=$\frac{1}{2}$QC=$\frac{1}{2}$(QB+10),根据相似三角形的性质得到$\frac{AD}{AB}=\frac{DP}{BQ}$,求出BQ=16,根据勾股定理即可得到结论.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠D=∠ABC=90°,∠DAB=90°,
∴∠ABQ=90°=∠D,
∵AQ⊥AP,
∴∠QAP=∠DAB=90°,
∴∠DAP=∠QAB=90°-∠BAP,
即∠QAB=∠DAP,∠ABQ=∠D,
∴△ADP∽△ABQ;
(2)解:作MN⊥QC,则∠QNM=∠QCD=90°,
又∵∠MQN=∠PQC
∴△MQN∽△PQC,
∴$\frac{MN}{PC}=\frac{QM}{QP}$,
∵∠C=∠MNQ=90°,
∴MN∥PC,
∵M为PQ的中点,
∴N为CQ的中点,
∴$\frac{MN}{PC}=\frac{1}{2}$,
又∵PC=DC-DP=20-8=12,
∴MN=$\frac{1}{2}$PC=6,QN=$\frac{1}{2}$QC=$\frac{1}{2}$(QB+10),
∵△ADP∽△ABQ
∴$\frac{AD}{AB}=\frac{DP}{BQ}$,
∴$\frac{10}{20}=\frac{8}{BQ}$,
∴BQ=16,
∵QN=$\frac{1}{2}$QC=13,
∴BN=QB-QN=3,
在Rt△MBN中,由勾股定理得:BM2=MN2+BN2=45,
∴BM=3$\sqrt{5}$.
点评 本题考查了矩形的性质,相似三角形的性质和判定,勾股定理的应用,能综合运用定理进行推理和计算是解此题的关键,题目比较好,难度偏大.

| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
②当x>1时,y的值随x值的增大而减小;
③x=2是方程ax2+(b-1)x+c=0的一个根;
④当-1<x<2时,ax2+(b-1)x+c>0.
上述结论中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
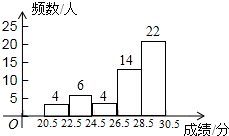 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )| A. | $\frac{9\sqrt{3}}{10}$cm | B. | $\frac{18\sqrt{3}}{10}$cm | C. | $\frac{9\sqrt{3}}{5}$cm | D. | $\frac{18\sqrt{3}}{5}$cm |

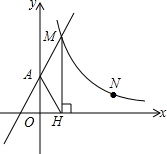 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.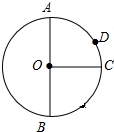 AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.
AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.