题目内容
3. 如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.
如图,四边形ABCD内接于⊙O过点A的切线与CD的延长线交于⊙O,且∠ADE=∠BDC.(1)求证:AC=BC;
(2)若AE=6,BC=12,CD=5,求AD的长.
分析 (1)根据圆内接四边形的性质得∠ADE=∠ABC,根据圆周角定理得∠BAC=∠BDC,然后利用∠ADE=∠BDC易得∠ABC=∠BAC,于是根据等腰三角形的判定即可得到结论;
(2)根据切割线定理得到EA2=ED•EC,则可计算出ED=4,然后证明△EAD∽△EAC,则可利用相似比计算出AD.
解答 (1)证明:∵∠ADE=∠ABC,∠BAC=∠BDC,
而∠ADE=∠BDC,
∴∠ABC=∠BAC,
∴AC=BC;
(2)解:∵EA为切线,EDC为割线,
∴EA2=ED•EC,
∴ED(5+ED)=36,解得ED=4,
即EA:ED=EC:EA,
而∠AED=∠CEA,
∴△EAD∽△EAC,
∴AD:AC=DE:AE,即AD:12=4:6,
∴AD=8.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.解决(2)小题的关键是根据切割线定理计算出DE,证明△EAD∽△EAC.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.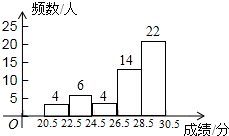 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
 九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )
九年级(3)班共有50名同学,如图是该班一次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数).若将不低于23分的成绩评为合格,则该班此次成绩达到合格的同学占全班人数的百分比是( )| A. | 80% | B. | 70% | C. | 92% | D. | 86% |
8.观察下列两个三位数的特点,猜想其中积的结果最大的是( )
| A. | 901×999 | B. | 922×978 | C. | 950×950 | D. | 961×939 |
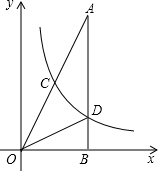 如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=$\frac{k}{x}$在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.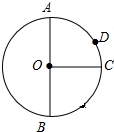 AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.
AB是⊙O的直径,且AB=2,OC⊥AB,垂足为点O,弧AD:弧DC=2:1,在OC上有一动点P,则PA+PD的最小值为$\sqrt{3}$.