题目内容
15.若等腰三角形底边上的高是底边的一半,则这个等腰三角形的顶角度数为90°.分析 作出图形,根据等腰三角形三线合一的性质可知底边上的高也是底边的中线,求出三角形被分成两个等腰直角三角形,求出两底角,再根据三角形的内角和定理即可求出顶角的度数.
解答 解:如图,根据题意,AD=$\frac{1}{2}$BC,
∵△ABC是等腰三角形,且AB=AC,AD⊥BC,
∴BD=CD,
∴△ABD,△ACD是等腰直角三角形,
∴∠B=∠C=45°,
∴∠BAC=180°-45°×2=90°,
即这个等腰三角形的顶角度数是90°.
故答案为:90°.
点评 本题考查了等腰三角形三线合一的性质,等腰三角形的两底角相等的性质,作出图形形象直观,更有助于问题的解决.

练习册系列答案
相关题目
6.下列各式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{4}$ |
3.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | 3.14 | D. | $\sqrt{5}$ |
20.下列计算正确的是( )
| A. | $\sqrt{2}×\sqrt{\frac{1}{2}}$=1 | B. | $\sqrt{4}-\sqrt{3}=1$ | C. | $\sqrt{6}÷\sqrt{3}$=2 | D. | $\sqrt{8}=±\sqrt{2}$ |
7.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{16}$ | B. | $\sqrt{5}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{7}}$ |
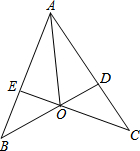 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.