Question

5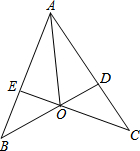．如图，BD⊥AC，CE⊥AB，垂足分别为D、E，BD与CE相交于点O，AO平分∠BAC．求证：OB=OC．

Answer 1

分析 根据角平分线的性质可以证得OE=OD，即可根据ASA证得△OBE≌△OCD，即可根据全等三角形的对应边相等证得OB=OC．

解答 证明：∵AO平分∠BAC，CE⊥AB于点E，BD⊥AC于点D，
∴OE=OD，
在直角△OBE和直角△OCD中，
$\left\{\begin{array}{l}{∠EOB=∠DOC}\\{∠BEO=∠ODC=90°}\\{OE=OD}\end{array}\right.$，
∴△OBE≌△OCD，
∴OB=OC．

点评 此题考查了角平分线的性质，把证明线段相等转化为证明三角形全等是常用的思路．