题目内容
7.下列各式不成立的是( )| A. | $5={(\sqrt{5})^2}$ | B. | $-y={(\sqrt{-y})^2}$(y<0) | C. | $-7={(\sqrt{-7})^2}$ | D. | -11=-$\sqrt{{{(-11)}^2}}$ |
分析 结合选项根据二次根式的乘除法的运算法则求解即可.
解答 解:A、$(\sqrt{5})$2=$\sqrt{5}$×$\sqrt{5}$=5,本选项错误;
B、∵y<0,∴-y>0,∴$(\sqrt{-y})$2=-y,本选项错误;
C、∵二次根式中被开方数为非负数,∴-7=($\sqrt{-7}$)2不成立,本选项正确;
D、-$\sqrt{{(-11)}^{2}}$=-$\sqrt{{11}^{2}}$=-11,本选项错误.
故选C.
点评 本题考查了二次根式的乘除法,解答本题的关键在于熟练掌握该知识点的运算法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.关于x的方程(a-1)x2+x+1=0是一元二次方程,则a的取值范围是( )
| A. | a≠1 | B. | a>-1且a≠1 | C. | a≥-1且a≠1 | D. | a为任意实数 |
16.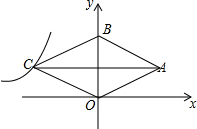 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | 12 | B. | 24 | C. | -12 | D. | -24 |
17.用代入法解方程组$\left\{\begin{array}{l}{3x+4y=2①}\\{2x-y=5②}\end{array}\right.$,能使代入后化简比较容易的变形是( )
| A. | 由①得x=$\frac{2-4y}{3}$ | B. | 由①得y=$\frac{2-3x}{4}$ | C. | 由②得x=$\frac{5+y}{2}$ | D. | 由②得y=2x-5 |
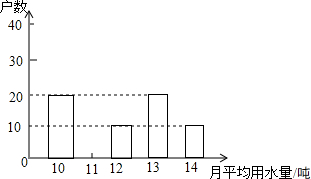 市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
市政府决定对市直机关800户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.