题目内容
12.一元二次方程x2-2x+k=0的一根为x1=-1,则另一根为3,k=-3.分析 设方程另一根为t,根据根与系数的关系得到-1•t=k,-1+t=2,然后解一次方程先求出t,再求k的值.
解答 解:设方程另一根为t,
根据题意得-1•t=k,-1+t=2,
解得t=3,k=-3,
故答案为:3,-3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
20.下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④调查运动员兴奋剂的使用情况.其中适合采用抽样调查的是( )
| A. | ① | B. | ② | C. | ③ | D. | ④ |
7.下列各式不成立的是( )
| A. | $5={(\sqrt{5})^2}$ | B. | $-y={(\sqrt{-y})^2}$(y<0) | C. | $-7={(\sqrt{-7})^2}$ | D. | -11=-$\sqrt{{{(-11)}^2}}$ |
17.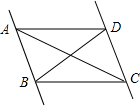 如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
 如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )
如图,给出下列四个条件:①∠DAC=∠ACB;②∠ABD=∠BDC;③∠BAD+∠CDA=180°;④∠ADC+∠BCD=180°.其中能判定AD∥BC的条件有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.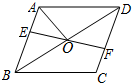 如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
 如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )
如图,在菱形ABCD中,E,F分别在AB,CD上,且BE=DF,EF与BD相交于点O,连结AO.若∠CBD=35°,则∠DAO的度数为( )| A. | 35° | B. | 55° | C. | 65° | D. | 75° |
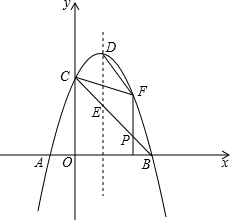 如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴相交于C点,顶点为D.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点(点A在点B的左侧),与y轴相交于C点,顶点为D. 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.