题目内容
16．
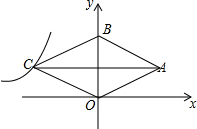菱形OABC的顶点O为原点，顶点B在y轴上，菱形的两条对角线的长分别是8和6（AC＞BO），反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点C，则k的值为（ ）| A． | 12 | B． | 24 | C． | -12 | D． | -24 |
分析 先根据菱形的性质求出C点坐标，再把C点坐标代入反比例函数的解析式即可得出k的值．
解答 解：∵菱形的两条对角线的长分别是8和6，
∴C（-4，3），
∵点C在反比例函数y=$\frac{k}{x}$（x＜0）的图象上，
∴3=$\frac{k}{-4}$，解得k=-12．
故选：C．
点评 本题考查的是反比例函数图象上点的坐标特点，即反比例函数图象上各点的坐标一定适合此函数的解析式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．下列各式不成立的是（ ）
| A． | $5={（\sqrt{5}）^2}$ | B． | $-y={（\sqrt{-y}）^2}$（y＜0） | C． | $-7={（\sqrt{-7}）^2}$ | D． | -11=-$\sqrt{{{（-11）}^2}}$ |
如图，已知矩形ABCD，AB=$\sqrt{3}$，BC=3，在BC上取两点E，F（E在F左边），以EF为边作等边三角形PEF，使顶点P在AD上，PE，PF分别交AC于点G，H．
11．小明解方程组$\left\{\begin{array}{l}{3x+y=●}\\{3x-y=10}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=6}\\{y=★}\end{array}\right.$，由于不小心滴上了两滴墨水，刚好遮住了两个数●和★，则这两个数分别为（ ）
| A． | 26和8 | B． | -26和8 | C． | 8和-26 | D． | -26和5 |
1．
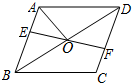如图，在菱形ABCD中，E，F分别在AB，CD上，且BE=DF，EF与BD相交于点O，连结AO．若∠CBD=35°，则∠DAO的度数为（ ）
如图，在菱形ABCD中，E，F分别在AB，CD上，且BE=DF，EF与BD相交于点O，连结AO．若∠CBD=35°，则∠DAO的度数为（ ）| A． | 35° | B． | 55° | C． | 65° | D． | 75° |
8．
如图，△OAB与△OA′B′位似，其中A、B的对应点分别为A′，B′，A′，B′均在图中正方形网格格点上，若线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为（ ）
如图，△OAB与△OA′B′位似，其中A、B的对应点分别为A′，B′，A′，B′均在图中正方形网格格点上，若线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为（ ）| A． | （$\frac{m}{2}，\frac{n}{2}$） | B． | （m，n） | C． | （2m，2n） | D． | （2n，2m） |