题目内容
11.附加题:先阅读下面解答过程,然后作答:形$\sqrt{m±2\sqrt{n}}$的化简,只要我们找到两个数a,b(a>b),使a+b=m,ab=n,则
$\sqrt{m±2\sqrt{n}}=\sqrt{a+b±2\sqrt{ab}}$=$\sqrt{(\sqrt{a})^{2}±2\sqrt{ab}+(\sqrt{b})^{2}}$=$\sqrt{(\sqrt{a}±\sqrt{b})^{2}}$=$\sqrt{a}$±$\sqrt{b}$
例:化简
$\sqrt{7+4\sqrt{3}}$=$\sqrt{7+2\sqrt{12}}$=$\sqrt{4+2\sqrt{4×3}+3}$=$\sqrt{(\sqrt{4})^{2}+2\sqrt{4×3}+(\sqrt{3})^{2}}$=$\sqrt{(\sqrt{4}+\sqrt{3})^{2}}$=2+$\sqrt{3}$
解:用上述例题方法的化简:(1)$\sqrt{13-2\sqrt{42}}$; (2)$\sqrt{7-\sqrt{40}}$; (3)$\sqrt{2-\sqrt{3}}$.
分析 根据阅读材料、利用二次根式的性质进行计算.
解答 解:(1)$\sqrt{13-2\sqrt{42}}$=$\sqrt{7-2\sqrt{7×6}+6}$=$\sqrt{(\sqrt{7})^{2}-2\sqrt{7×6}+({\sqrt{6})}^{2}}$=$\sqrt{(\sqrt{7}-\sqrt{6})^{2}}$=$\sqrt{7}$-$\sqrt{6}$;
(2)$\sqrt{7-\sqrt{40}}$=$\sqrt{5-2\sqrt{5×2}+2}$=$\sqrt{(\sqrt{5}-\sqrt{2})^{2}}$=$\sqrt{5}$-$\sqrt{2}$;
(3)$\sqrt{2-\sqrt{3}}$=$\sqrt{\frac{3}{2}-2\sqrt{\frac{3}{2}×\frac{1}{2}}+\frac{1}{2}}$=$\sqrt{({\frac{\sqrt{6}}{2}-\frac{\sqrt{2}}{2})}^{2}}$=$\frac{\sqrt{6}}{2}-\frac{\sqrt{2}}{2}$.
点评 本题考查的是二次根式的性质与化简,掌握二次根式的性质:$\sqrt{{a}^{2}}$=a(a≥0)是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
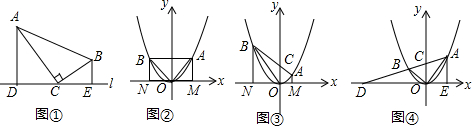
19.原型:如图①,在Rt△ABC中,∠ACB=90°,C是在直线l上的一点,AD⊥l,BE⊥l,垂足分别为D、E.易证△ACD∽△CBE.(不需证明)
应用:点A、B在抛物线y=x2上,且OA⊥OB,连结AB与y轴交于点C,点C的坐标为(0,d).过点A、B分别作x轴的垂线,垂足为M、N,点M、N的坐标分别为(m,0)、(n,0).
(1)当OA=OB时,如图②,m=1,d=1;
当OA≠OB,如图③,m=$\frac{2}{3}$时,d=1.
(2)若将抛物线“y=x2”换成“y=2x2”,其他条件不变,当OA=OB时,d=$\frac{1}{2}$;当OA≠OB,m=1时,d=$\frac{1}{2}$.
探究:若将抛物线“y=x2”换成“y=ax2(a>0)”,其他条件不变,解答下列问题:
(1)完成下列表格.
(2)猜测d与a的关系,并证明其结论.
拓展:如图④,点A、B在抛物线y=ax2(a>0)上,且OA⊥OB,连结AB与y轴关于点C,AB的延长线与x轴交于点D.AE⊥x轴,垂足为E,当AE=$\frac{4}{3a}$时,△AOE与△CDO的面积之比为4:9.
应用:点A、B在抛物线y=x2上,且OA⊥OB,连结AB与y轴交于点C,点C的坐标为(0,d).过点A、B分别作x轴的垂线,垂足为M、N,点M、N的坐标分别为(m,0)、(n,0).
(1)当OA=OB时,如图②,m=1,d=1;
当OA≠OB,如图③,m=$\frac{2}{3}$时,d=1.
(2)若将抛物线“y=x2”换成“y=2x2”,其他条件不变,当OA=OB时,d=$\frac{1}{2}$;当OA≠OB,m=1时,d=$\frac{1}{2}$.
探究:若将抛物线“y=x2”换成“y=ax2(a>0)”,其他条件不变,解答下列问题:
(1)完成下列表格.
| a | 1 | 2 | 3 | $\frac{1}{2}$ |
| d | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ | 2 |
拓展:如图④,点A、B在抛物线y=ax2(a>0)上,且OA⊥OB,连结AB与y轴关于点C,AB的延长线与x轴交于点D.AE⊥x轴,垂足为E,当AE=$\frac{4}{3a}$时,△AOE与△CDO的面积之比为4:9.

1.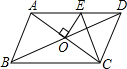 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
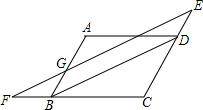 如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.
如图,在?ABCD中,直线EF∥BD,与CD、CB的延长线分别交于点E、F,交AB、AD于G、H.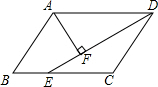 如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°.
如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°.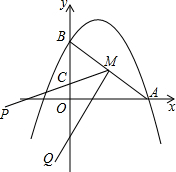 如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B.
如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B.