题目内容
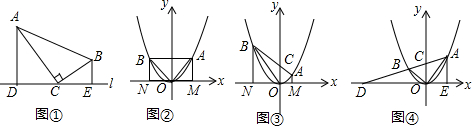
19.原型:如图①,在Rt△ABC中,∠ACB=90°,C是在直线l上的一点,AD⊥l,BE⊥l,垂足分别为D、E.易证△ACD∽△CBE.(不需证明)应用:点A、B在抛物线y=x2上,且OA⊥OB,连结AB与y轴交于点C,点C的坐标为(0,d).过点A、B分别作x轴的垂线,垂足为M、N,点M、N的坐标分别为(m,0)、(n,0).
(1)当OA=OB时,如图②,m=1,d=1;
当OA≠OB,如图③,m=$\frac{2}{3}$时,d=1.
(2)若将抛物线“y=x2”换成“y=2x2”,其他条件不变,当OA=OB时,d=$\frac{1}{2}$;当OA≠OB,m=1时,d=$\frac{1}{2}$.
探究:若将抛物线“y=x2”换成“y=ax2(a>0)”,其他条件不变,解答下列问题:
(1)完成下列表格.
| a | 1 | 2 | 3 | $\frac{1}{2}$ |
| d | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ | 2 |
拓展:如图④,点A、B在抛物线y=ax2(a>0)上,且OA⊥OB,连结AB与y轴关于点C,AB的延长线与x轴交于点D.AE⊥x轴,垂足为E,当AE=$\frac{4}{3a}$时,△AOE与△CDO的面积之比为4:9.
分析 (1)如图②中,根据条件利用相似三角形的性质求出点B坐标以及求出直线AB与y轴的交点,点M的坐标即可.
(2)如图③中,由题意A($\frac{2}{3}$,$\frac{4}{9}$),设B(k,k2)由△AOM∽△OBN,得$\frac{AM}{ON}=\frac{OM}{BN}$,求出点B坐标,再求出直线AB与y轴的交点即可解决问题
探究:(1)利用相似三角形性质求出点B坐标,再求出直线AB与y轴的交点即可解决问题.
(2)如图④中,结论:d=$\frac{1}{a}$,由点A(m,am2),点B(n,an2)的坐标,求出直线AB的解析式,再利用△AOM∽△OBN得$\frac{AM}{ON}=\frac{OM}{BN}$,得出mn与a的关系即可解决问题.
解答 解:(1)如图②中,∵OA=OB,∠AOB=90°,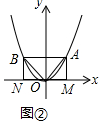
∴A、B关于y轴得出,
∴AB∥MN,
∴可以设点A坐标(x,x),
∴x=x2,
∵x≠0,
∴x=1,
∴m=1,d=1.
如图③中,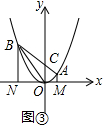 由题意A($\frac{2}{3}$,$\frac{4}{9}$),设B(k,k2).
由题意A($\frac{2}{3}$,$\frac{4}{9}$),设B(k,k2).
∵△AOM∽△OBN,
∴$\frac{AM}{ON}=\frac{OM}{BN}$,
∴$\frac{\frac{4}{9}}{-k}=\frac{\frac{2}{3}}{{k}^{2}}$,
∴k=-$\frac{3}{2}$,
∴点B坐标(-$\frac{3}{2}$,$\frac{9}{4}$),设直线AB为y=k′x+b则$\left\{\begin{array}{l}{\frac{2}{3}k+b=\frac{4}{9}\\;}\\{-\frac{3}{2}k+b=\frac{9}{4}}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{5}{6}}\\{b=1}\end{array}\right.$,
∴直线AB为y=-$\frac{5}{6}x$+1,
∴d=1.
故答案为1,1,1.
(2)若将抛物线“y=x2”换成“y=2x2”,其他条件不变,当OA=OB时,如图2,∵OA=OB,∠AOB=90°,
∴A、B关于y轴得出,
∴AB∥MN,
∴可以设点A坐标(x,x),
∴x=2x2,
∵x≠0,
∴x=$\frac{1}{2}$,
∴d=$\frac{1}{2}$,
当OA≠OB,m=1时,如图3中,点A(1,2),设B(k,2k2).
∵△AOM∽△OBN,
∴$\frac{AM}{ON}=\frac{OM}{BN}$,
∴$\frac{2}{-k}$=$\frac{1}{2{k}^{2}}$,
∴k=-$\frac{1}{4}$,
∴点B(-$\frac{1}{4}$,$\frac{1}{8}$),
∵直线AB为y=$\frac{3}{2}$x+$\frac{1}{2}$.
∴点C坐标为(0,$\frac{1}{2}$),
∴d=$\frac{1}{2}$.
故答案为$\frac{1}{2}$,$\frac{1}{2}$.
探究(1)同理可以得到d=$\frac{1}{3}$,d=2.
故答案为$\frac{1}{3}$,2.
(2)结论:d=$\frac{1}{a}$.
证明:∵M(m,0),N(n,0),点A、B都在抛物线上,
∴点A(m,am2),点B(n,an2),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{mk+b=a{m}^{2}}\\{nk+b=a{n}^{2}}\end{array}\right.$解得$\left\{\begin{array}{l}{k=(m+n)}\\{b=-amn}\end{array}\right.$,
又∵△AOM∽△OBN,
∴$\frac{AM}{ON}=\frac{OM}{BN}$,
∴$\frac{a{n}^{2}}{-n}$=$\frac{m}{a{m}^{2}}$,
∴mn=-$\frac{1}{{a}^{2}}$,
∴b=-a(-$\frac{1}{{a}^{2}}$)=$\frac{1}{a}$.
(2)如图④中,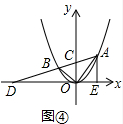 ∵AE=$\frac{4}{3a}$,
∵AE=$\frac{4}{3a}$,
∴$\frac{4}{3a}$=ax2,
∴x=±$\frac{2\sqrt{3}}{3a}$,
∴OE=$\frac{2\sqrt{3}}{3a}$,
∵OC=$\frac{1}{a}$,OC∥AE,
∴$\frac{OC}{AE}$=$\frac{DO}{DE}$,
∴$\frac{\frac{1}{a}}{\frac{4}{3a}}$=$\frac{DO}{DO+\frac{2\sqrt{3}}{3a}}$,
∴DO=$\frac{2\sqrt{3}}{a}$,
∴S△AOE=$\frac{1}{2}$•OE•AE=$\frac{1}{2}$$•\frac{2\sqrt{3}}{3a}$•$\frac{4}{3a}$=$\frac{4\sqrt{3}}{9{a}^{2}}$,S△DOC=$\frac{1}{2}$•DO•CO=$\frac{1}{2}$•$\frac{2\sqrt{3}}{a}$$•\frac{1}{a}$=$\frac{\sqrt{3}}{{a}^{2}}$,
∴S△AOE:S△DOC=4:9.
点评 本题考查二次函数综合题、相似三角形的性质、一次函数的有关知识,解题的关键是学会待定系数法确定函数解析式,利用相似三角形的性质建立方程解决问题,学会用参数解决问题,属于中考压轴题,有一定的难度.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
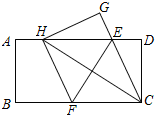 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: 如图,已知三角形ABC及三角形ABC外一点D,平移三角形ABC,使点A移动到点D,并保留画图痕迹.
如图,已知三角形ABC及三角形ABC外一点D,平移三角形ABC,使点A移动到点D,并保留画图痕迹.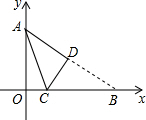 已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).
已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).