题目内容
1.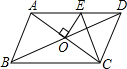 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
分析 根据平行四边形性质得出AD=BC,AB=CD,OA=OC,根据线段垂直平分线得出AE=CE,求出CD+DE+EC=AD+CD,代入求出即可.
解答 解:∵平行四边形ABCD,
∴AD=BC,AB=CD,OA=OC,
∵EO⊥AC,
∴AE=EC,
∵AB+BC+CD+AD=16cm,
∴AD+DC=8cm,
∴△DCE的周长是:CD+DE+CE=AE+DE+CD=AD+CD=8(cm),
故选:B.
点评 本题考查了平行四边形性质、线段垂直平分线性质的应用,关键是求出AE=CE,主要培养学生运用性质进行推理的能力,

练习册系列答案
相关题目
9.?ABCD中,∠A=4∠B,则∠D的度数是( )
| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
13.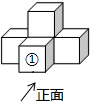 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )| A. | 主视图与左视图不变 | B. | 左视图与俯视图不变 | ||
| C. | 主视图与俯视图改变 | D. | 左视图与俯视图改变 |
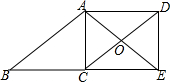 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.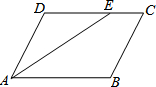 如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.
如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.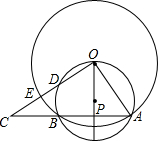 如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.
如图,⊙O与过点O的⊙P交于AB,D是⊙P的劣弧OB上一点,射线OD交⊙O于点E,交AB延长线于点C.如果AB=24,tan∠AOP=$\frac{2}{3}$.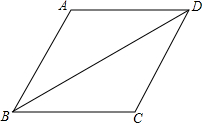 如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.