题目内容
2.已知实数x、y满足$\sqrt{x+2}$+(y-1)2=0,则$\root{3}{x+y}$=-1.分析 利用非负数的性质列出方程组,求出方程组的解得到x与y的值,即可确定出原式的值.
解答 解:∵$\sqrt{x+2}$+(y-1)2=0,
∴$\left\{\begin{array}{l}{x+2=0}\\{y-1=0}\end{array}\right.$,
解得:x=-2,y=1,
则原式=-1,
故答案为:-1
点评 此题考查了立方根,以及非负数的性质,熟练掌握立方根定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
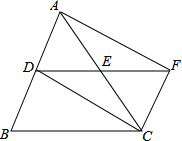 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.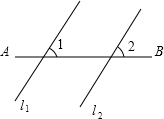 如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是50°.
如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是50°.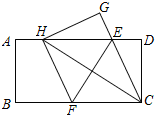 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E、F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论: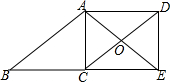 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.