题目内容
6.若$y=\frac{{\sqrt{x-4}+\sqrt{4-x}}}{2}-2$,则(x+y)-2=$\frac{1}{4}$.分析 根据二次根式有意义的条件列出不等式,求出x的值,代入已知式子求出y的值,根据负整数指数幂的运算法则计算即可.
解答 解:由题意得,x-4≥0,4-x≥0,
解得,x=4,
则y=-2,
∴(x+y)-2=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数是非负数是解题的关键.

练习册系列答案
相关题目
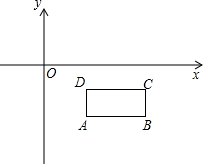 如图,已知矩形ABCD四个顶点的坐标分别是A(2,$-2\sqrt{2}$),B(5,$-2\sqrt{2}$),C(5,$-\sqrt{2}$),D(2,$-\sqrt{2}$)
如图,已知矩形ABCD四个顶点的坐标分别是A(2,$-2\sqrt{2}$),B(5,$-2\sqrt{2}$),C(5,$-\sqrt{2}$),D(2,$-\sqrt{2}$)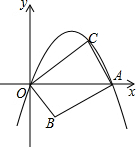 如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.
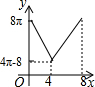
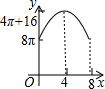
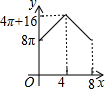
如图,在平面直角坐标系中,抛物线y=-x2+mx(m>0且m≠1)与x轴交于原点O和点A,点B的坐标为(1,-1),连结AB,将线段AB绕点A顺时针旋转90°得到线段AC,连结OB、OC.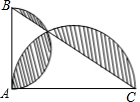 如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )
如图,△ABC中,∠BAC=90°,AC+AB=8,以AC、AB为半径作半圆.记图中阴影部分面积为y,AC为x,则下列y关于x的图象正确的是( )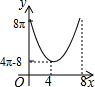
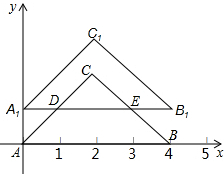 如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.
如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.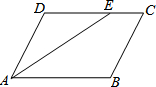 如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.
如图:在?ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=27°,求∠C、∠B的度数.