题目内容
20.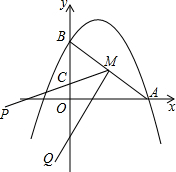 如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B.
如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B.(1)求点A,点B的坐标及AB的长;
(2)已知M为AB的中点,∠PMQ在AB的同侧以点M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D,设AD的长为m(m>0),BC的长为n.
①求n随m变化的函数解析式;
②若点E(-k-1,-k2+1)在抛物线y=-$\frac{1}{2}$x2+x+4上,且点E不在坐标轴上,当m,n为何值时,∠PMQ的边过点E?
分析 (1)由坐标轴上点的特点计算即可;
(2)①判断出∠AMD=∠BCM,∠OAB=∠OBA得到△ADM∽△BMC,得出比例式即可;
②E(-k-1,-k2+1)在抛物线y=-$\frac{1}{2}$x2+x+4上,求出k值,然后分两种情况讨论.
解答 解:(1)令y=0,得到0=-$\frac{1}{2}$x2+x+4,
∴x1=-1,x2=4,
∵点A在x轴正半轴,
∴A(4,0),
令x=0,得y=4,
∴B(0,4),
在Rt△AOB中,OA=4,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4$\sqrt{2}$;
(2)①由(1)有,OA=OB,
∴∠OAB=∠OBA,
∵∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵∠PMA=∠OBA+∠BCM,
∴∠AMD+∠CMD=∠ABO+∠BCM,
∴∠AMD=∠BCM,
∵∠OAB=∠OBA,
∴△ADM∽△BMC,
∴$\frac{AD}{BM}=\frac{AM}{BC}$,
由(1)有,AB=4$\sqrt{2}$,
∵M为AB中点,
∴AM=BM=2$\sqrt{2}$,
∴$\frac{m}{2\sqrt{2}}\frac{2\sqrt{2}}{n}$,
∴n=$\frac{8}{m}$(m>0),
②∵E(-k-1,-k2+1)在抛物线y=-$\frac{1}{2}$x2+x+4上,
∴k1=1,k2=3,
当k=1时,-k-1=-2,-k2+1=0,
∴(-2,0)在坐标轴上,不符合题意,
当k=3时,-k-1=-4,-k2+1=-8,
∴点E(-4,-8),
设直线ME解析式为y=mx+n,
∵点M(2,2),
∴$\left\{\begin{array}{l}{2m+n=2}\\{-4m+n=-8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=\frac{5}{3}}\\{n=-\frac{4}{3}}\end{array}\right.$,
∴直线ME的解析式为y=$\frac{5}{3}$x-$\frac{4}{3}$,
直线ME与x轴的交点为($\frac{4}{5}$,0)与y轴的交点为(0,-$\frac{4}{3}$),
当∠PMQ的边MP过点E(-4,-8),
∴C(0,-$\frac{4}{3}$),
∴B(0,4),
∴n=4-(-$\frac{4}{3}$)=$\frac{16}{3}$,
m=$\frac{8}{n}$=$\frac{3}{2}$,
∴m=$\frac{3}{2}$,n=$\frac{16}{3}$,
当∠PMQ的边MQ过点E(-4,-8),
∴D($\frac{4}{5}$,0),
∵A(4,0)
∴m=AD=4-$\frac{4}{5}$=$\frac{16}{5}$,
∵n=$\frac{8}{m}$=$\frac{5}{2}$,
∴m=$\frac{16}{5}$,n=$\frac{5}{2}$,
即:m=$\frac{3}{2}$,n=$\frac{16}{3}$;m=$\frac{16}{5}$,n=$\frac{5}{2}$,
点评 此题是二次函数综合题,考查了坐标轴上点的特点,相似三角形的性质和判定,待定系数法确定函数解析式,确定点的坐标是解本题的关键,确定函数解析式是本题的难点.

| A. | $\frac{1}{2}$,1 | B. | -$\frac{1}{2}$,1 | C. | -$\frac{1}{2}$,-1 | D. | $\frac{1}{2}$,-1 |
| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
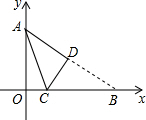 已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).
已知OA=6,OB=8,将△AOB沿着某直线CD折叠后如图所示,CD与x轴交于点C,与AB交于点D,则点C坐标是($\frac{7}{4}$,0).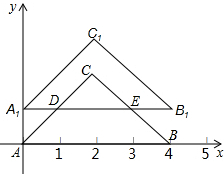 如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.
如图,等腰直角三角形ABC中,∠C=90°,A(0,0),B(4,0),点C在x轴上方,把△ABC向上平移1个单位后,得到△A1B1C1,且A1B1分别交AC于点D,交BC于点E.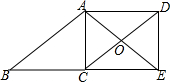 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.