题目内容
1. 一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,
一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,(1)建立适当的直角坐标系,求拱形隧道的抛物线关系式
(2)拱形隧道下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m,高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
分析 (1)根据题意可知A,B,C的坐标,设出抛物线的解析式代入可求解;
(2)把x=7代入(1)的函数表达式,求出y的值即可判断.
解答 解:(1)如图,以AB所在直线为x轴,线段AB中垂线为y轴建立平面直角坐标系,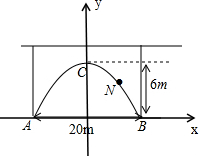
根据题意知A,B,C的坐标分别是(-10,0),(10,0),(0,6),
设抛物线的解析式为y=ax2+c,
将B,C的坐标代入y=ax2+c,
得$\left\{\begin{array}{l}{c=6}\\{100a+c=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-\frac{3}{50}}\\{c=6}\end{array}\right.$,
所以抛物线的表达式y=-$\frac{3}{50}$x2+6.
(2)根据题意,三辆汽车最右边到原点的距离为:1+3×2=7,
当x=7是,y=-$\frac{3}{50}$×49+6=3.06>3,
故可以并排行驶宽2m,高3m的三辆汽车.
点评 本题考查的是点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题是关键.

练习册系列答案
相关题目
6.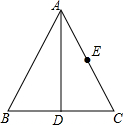 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,CD=6,BD=4,则AD=9.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,CD=6,BD=4,则AD=9.