题目内容
6.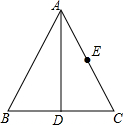 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | 1 | B. | 1.5 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 先根据锐角三角函数的定义求出AB的长,连接BE,则线段BE的长即为QE+QC最小值.
解答 解:∵△ABC是等边三角形,AD⊥BC,且BC=2,
∴AB=2,
连接BE,线段BE的长即为QE+QC最小值,
∵点E是边AB的中点,
∴CE=$\frac{1}{2}$AB=1,
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{3}$,
∴QE+QC的最小值是$\sqrt{3}$.
故选D
点评 本题考查的是轴对称-最短路线问题,熟知等边三角形的性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.多项式-x2-$\frac{1}{2}$x-1的各项分别是( )
| A. | -x2,$\frac{1}{2}$x,1 | B. | -x2,-$\frac{1}{2}$x,-1 | C. | x2,$\frac{1}{2}$x,1 | D. | 以上答案都不对 |
16.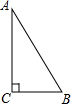 如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
 如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )
如图,Rt△ABC中,BC=2,AC=2$\sqrt{3}$,则AB长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
 一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,
一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,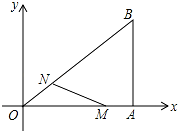 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题: