题目内容
13.已知关于x的一元二次方程x2-(2k+3)x+k2+3k+2=0(1)试判断上述方程根的情况.
(2)若以上述方程的两个根为横坐标、纵坐标的点恰在反比例函数$y=\frac{m}{x}$的图象上,求满足条件的m的最小值.
分析 (1)表示出方程根的判别式,根据根的判别式的正负即可确定出方程根的情况;
(2)设方程的两根为x1,x2,根据题意得m=x1x2,再利用根与系数关系表示出x1x2,列出m关于k的二次函数解析式,利用二次函数性质求出m的最小值即可;
解答 解:∵△=b2-4ac=(2k+3)2-4×(k2+3k+2)=1>0,
∴方程有两个相等实数根;
(2)(2)设方程x2-(2k+3)x+k2+3k+2=0的两个根为x1,x2,根据题意得m=x1x2,
又由一元二次方程根与系数的关系得x1x2=k2+3k+2,
∴m=k2+3k+2=(k+$\frac{3}{2}$)2-$\frac{1}{4}$,
则当k=-$\frac{3}{2}$时,m取得最小值-$\frac{1}{4}$.
点评 本题考查了一元二次方程根与系数的关系,根的情况判断,二次函数的性质,勾股定理,以及等腰三角形的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.一个三位数,百位上的数字是a,十位上的数字是a的2倍,个位上的数字比十位上的数字小1,这个三位数用代数式可以表示为( )
| A. | 122a-1 | B. | 113a-1 | C. | 5a-1 | D. | 111a-1 |
5.下列方程是一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | 3x2-2x=3(x2-2) | C. | x3-2x-4=0 | D. | (x-1)2-1=0 |
 一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,
一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,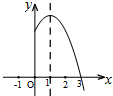 已知二次函数y=-2x2+4x+m的部分图象如图所示,则关于x的一元二次方程-2x2+4x+m=0的解是x1=-1,x2=3.
已知二次函数y=-2x2+4x+m的部分图象如图所示,则关于x的一元二次方程-2x2+4x+m=0的解是x1=-1,x2=3.