题目内容
在一个直角三角形中，有一个锐角等于30°，则另一个锐角的大小为______度．
60
【解析】【解析】
∵三角形是直角三角形，一个锐角等于30°，∴另一个锐角为90°﹣30°=60°．
故答案为：60．
练习册系列答案
小题狂做系列答案
相关题目
已知方程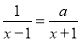
的解为x=2，求
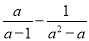的值．
， .
【解析】试题分析：根据分式方程的解为x=2，代入到分式方程，求出a的值，把通分化简，再把a的值代入计算即可求出代数式的值．
把x=2代入得，a=3，
∴原式=﹣
=
=，
当a=3时，原式==． 右图中四边形均为长方形，根据图形，写出一个正确的等式：_____________．
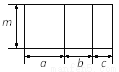
m（a+b+c）=ma+mb+mc（答案不唯一）．
【解析】试题分析：从两方面计算该图形的面积即可求出该等式
本题解析：从整体来计算矩形的面积：m(a+b+c)，
从部分来计算矩形的面积：ma+mb+mc，
所以m(a+b+c)=ma+mb+mc
故答案为：m(a+b+c)=ma+mb+mc 下列现象：(1)电风扇的转动；(2)打气筒打气时，活塞的运动；(3)钟摆的摆动；(4)传送带上瓶装饮料的移动．其中属于平移的是_________．
(2)(4)
【解析】试题分析：（1）电风扇的转动是旋转，不属于平移；
（2）打气筒打气时，活塞的运动属于平移；
（3）钟摆的摆动是旋转，不属于平移；
（4）传送带上瓶装饮料的移动符合平移的性质，属于平移．
故选D． 如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B；求证：CD⊥AB；
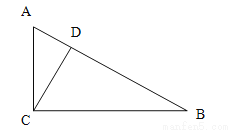
证明过程见解析
【解析】试题分析：根据∠ACB=90°得出∠A+∠B=90°，结合已知条件得出∠A+∠ACD=90°，从而得出答案.
试题解析：∵∠ACB=90° ∴∠A+∠B=90° ∵∠ACD=∠B ∴∠A+∠ACD=90° ∴∠ADC=90°
∴CD⊥AB 已知，如图，△ABC中，∠BAC=90°，AD⊥BC于D，则图中相等的锐角的对数有（ ）
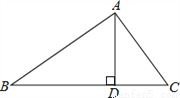
A. 4对 B. 3对 C. 2对 D. 1对
C
【解析】【解析】
相等的锐角有：∠B=∠CAD，∠C=∠BAD共2对．故选C． 如图，O是∠BAC内一点，且点O到AB，AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
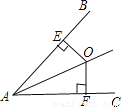
A.HL B.AAS C.SSS D.ASA
A
【解析】
试题分析：利用点O到AB，AC的距离OE=OF，可知△AEO和△AFO是直角三角形，然后可直接利用HL求证△AEO≌△AFO，即可得出答案．
【解析】
∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO．
故选A． 如图所示，在△ABC中，AB＝AC，点D在AC上，且BD＝BC＝AD，则∠A等于( )
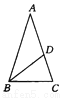
A. 30° B. 40° C. 45° D. 36°
D
【解析】∵AD＝BD，
∴∠A＝∠ABD，
∴∠BDC＝2∠A.
∵BD＝BC，
∴∠C＝∠BDC＝2∠A．
∵AB＝AC，
∴∠ABC＝∠C＝2∠A，
由三角形内角和定理，得∠A+2∠A+2∠A＝180°，
即∠A＝36°．
故选D. 下列说法正确的是（ ）
A. x=4是不等式2x＞－8的一个解 B. x=－4是不等式2x＞－8的解集
C. 不等式2x＞－8的解集是x＞4 D. 2x＞－8的解集是x＜－4
A
【解析】根据不等式的基本性质，可知2x＞-8的解集为x＞-4，所以x=4是它的一个解；x=-4不是其解集.
故选：A.