��Ŀ����
��ͼ��ʾ����ABC������MN����ƽ��һ��������Ϊ��A��B��C�䣮�ҳ�������������ƽ������ȵ��߶��Լ�ȫ�ȵ������Σ�
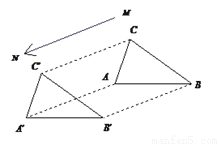
 AB��A��B�䣻BC��B��C�䣻AC��A��C�䣻��ABC�ա�A��B��C��
���������������������ƽ��ǰ������ͼ�εĶ�Ӧ�߶�ƽ������ȿ���ֱ���ҳ�������������ƽ������ȵ��߶Σ�����ƽ��ǰ�������ͼ��ȫ�ȿ�ֱ֪���ҳ�ȫ�ȵ������Σ�
���������
��������
������������ƽ������ȵ��߶��У�AB��A��B����BC��B��C����AC��A��C����
ȫ�ȵ��������ǣ���ABC�ա�A��B��C����...
AB��A��B�䣻BC��B��C�䣻AC��A��C�䣻��ABC�ա�A��B��C��
���������������������ƽ��ǰ������ͼ�εĶ�Ӧ�߶�ƽ������ȿ���ֱ���ҳ�������������ƽ������ȵ��߶Σ�����ƽ��ǰ�������ͼ��ȫ�ȿ�ֱ֪���ҳ�ȫ�ȵ������Σ�
���������
��������
������������ƽ������ȵ��߶��У�AB��A��B����BC��B��C����AC��A��C����
ȫ�ȵ��������ǣ���ABC�ա�A��B��C����...
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д����ַ����������������ѡ��һ�����������
��1����һֱ��������Ϊ������ͼ�Ρ���������ת���õ�һ���糵�����ͼ����������Ƴ����ַ糵����ͼ���أ��뽫���ͼ������������ɺ���ͬѧ���н�����
��2������Բ�������Ρ��������Σ�ͨ��ƽ�ƻ���ת�����һ��ͼ������ɺ���ͬѧ���������Ʒ��˵����������ͼ��
 ������
�����������������������ת�ĽǶȲ�ͬ�ɵõ���ͬ�ķ糵��״��ֻҪ�������⼴�ɣ�
�����������������
ѡ��1��������������ת90��������
������
�����������������������ת�ĽǶȲ�ͬ�ɵõ���ͬ�ķ糵��״��ֻҪ�������⼴�ɣ�
�����������������
ѡ��1��������������ת90�������� �ڡ�ABC�У���C��90�㣬AB��13��BC��5����tanB��________��
 ���������ߡ�C=90�㣬AB=13��BC=5����AC==12����tanB=��
�ʴ�Ϊ�� .
���������ߡ�C=90�㣬AB=13��BC=5����AC==12����tanB=��
�ʴ�Ϊ�� . ��ͼ���ı��ξ�Ϊ�����Σ�����ͼ�Σ�д��һ����ȷ�ĵ�ʽ��_____________��
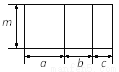
 m��a+b+c��=ma+mb+mc���𰸲�Ψһ����
�����������������������������ͼ�ε������������õ�ʽ
����������������������������m(a+b+c)��
�Ӳ�����������ε������ma+mb+mc��
����m(a+b+c)=ma+mb+mc
�ʴ�Ϊ��m(a+b+c)=ma+mb+mc
m��a+b+c��=ma+mb+mc���𰸲�Ψһ����
�����������������������������ͼ�ε������������õ�ʽ
����������������������������m(a+b+c)��
�Ӳ�����������ε������ma+mb+mc��
����m(a+b+c)=ma+mb+mc
�ʴ�Ϊ��m(a+b+c)=ma+mb+mc ����ʽ15m3n2+5m2n��20m2n3�Ĺ���ʽ�ǣ����� ��
A. 5mn B. 5m2n2 C. 5m2n D. 5mn2
 C
������������ʽ15n²+5m²n?20m² �У�
����ϵ�������Լ����5��
������е���ͬ��ĸ��m��n����ĸm��ָ�������2����ĸn��ָ�������1��
�������Ĺ���ʽ��5m²n.
��ѡC.
C
������������ʽ15n²+5m²n?20m² �У�
����ϵ�������Լ����5��
������е���ͬ��ĸ��m��n����ĸm��ָ�������2����ĸn��ָ�������1��
�������Ĺ���ʽ��5m²n.
��ѡC. ��������(1)����ȵ�ת����(2)����Ͳ����ʱ���������˶���(3)�Ӱڵİڶ���(4)���ʹ���ƿװ���ϵ��ƶ�����������ƽ�Ƶ���_________��
 (2)(4)
�������������������1������ȵ�ת������ת��������ƽ�ƣ�
��2������Ͳ����ʱ���������˶�����ƽ�ƣ�
��3���Ӱڵİڶ�����ת��������ƽ�ƣ�
��4�����ʹ���ƿװ���ϵ��ƶ�����ƽ�Ƶ����ʣ�����ƽ�ƣ�
��ѡD��
(2)(4)
�������������������1������ȵ�ת������ת��������ƽ�ƣ�
��2������Ͳ����ʱ���������˶�����ƽ�ƣ�
��3���Ӱڵİڶ�����ת��������ƽ�ƣ�
��4�����ʹ���ƿװ���ϵ��ƶ�����ƽ�Ƶ����ʣ�����ƽ�ƣ�
��ѡD�� ��ͼ����Rt��ABC�У���ACB=90�㣬D��AB��һ�㣬�ҡ�ACD=��B����֤��CD��AB��
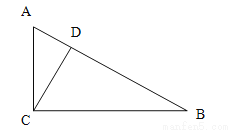
 ֤�����̼�����
��������������������ݡ�ACB=90��ó���A+��B=90�㣬�����֪�����ó���A+��ACD=90�㣬�Ӷ��ó���.
����������ߡ�ACB=90�� ���A+��B=90�� �ߡ�ACD=��B ���A+��ACD=90�� ���ADC=90��
��CD��AB
֤�����̼�����
��������������������ݡ�ACB=90��ó���A+��B=90�㣬�����֪�����ó���A+��ACD=90�㣬�Ӷ��ó���.
����������ߡ�ACB=90�� ���A+��B=90�� �ߡ�ACD=��B ���A+��ACD=90�� ���ADC=90��
��CD��AB ��ͼ��O�ǡ�BAC��һ�㣬�ҵ�O��AB��AC�ľ���OE=OF�����AEO�ա�AFO�������ǣ� ��
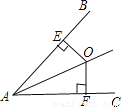
A.HL B.AAS C.SSS D.ASA
 A
��������
������������õ�O��AB��AC�ľ���OE=OF����֪��AEO�͡�AFO��ֱ�������Σ�Ȼ���ֱ������HL��֤��AEO�ա�AFO�����ɵó��𰸣�
��������
��OE��AB��OF��AC�����AEO=��AFO=90�㣬
�֡�OE=OF��AOΪ�����ߣ����AEO�ա�AFO��
��ѡA��
A
��������
������������õ�O��AB��AC�ľ���OE=OF����֪��AEO�͡�AFO��ֱ�������Σ�Ȼ���ֱ������HL��֤��AEO�ա�AFO�����ɵó��𰸣�
��������
��OE��AB��OF��AC�����AEO=��AFO=90�㣬
�֡�OE=OF��AOΪ�����ߣ����AEO�ա�AFO��
��ѡA�� ���м����˶�����ƽ�Ƶ��ǣ� ��
��ˮƽ������ϵ�ש���˶�����ơ���������ϵ�ơ��ͨ��ѹ�ǻ�ǰ����˶�������������������е�˶�����������������˶�
A. һ�� B. ���� C. ���� D. ����
 B
�������������������1���ͣ�3���������˶����Կ����������ƽ�ƣ���2���ͣ�4������ƽ���˶���
��ѡB.
B
�������������������1���ͣ�3���������˶����Կ����������ƽ�ƣ���2���ͣ�4������ƽ���˶���
��ѡB. 
