题目内容
5.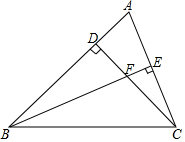 如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.(1)判断△DBC的形状并证明你的结论.
(2)求证:BF=AC.
(3)试说明CE=$\frac{1}{2}$BF.
分析 (1)根据已知条件得到∠BCD=45°,求得BD=CD,于是得到结论;
(2)根据全等三角形的性质和判定即可得到结论;
(3)根据线段垂直平分线的性质即可得到结论.
解答 解:(1)△DBC是等腰直角三角形,
理由:∵∠ABC=45°,CD⊥AB,
∴∠BCD=45°,
∴BD=CD,
∴△DBC是等腰直角三角形;
(2)∵BE⊥AC,
∴∠BDC=∠BEC=90°,
∵∠BFD=∠CFE,
∴∠DBF=∠ACD,
在△BDF与△ACD中,$\left\{\begin{array}{l}{∠BDC=∠ADC=90°}\\{∠DBF=∠DCA}\\{BD=CD}\end{array}\right.$,
∴△BDF≌△ACD,
∴BF=AC;
(3)∵BE是AC的垂直平分线,
∴CE=$\frac{1}{2}$AC,
∴CE=$\frac{1}{2}$BF.
点评 本题考查了线段垂直平分线的性质,全等三角形的性质,等腰直角三角形的判定,正确的识别图形是解题的关键.

练习册系列答案
相关题目
20.公交车沿东西方向行驶,如果把车站的起点记为0,向东行驶记为正,向西行驶记为负,其中一辆车出发以后行驶的路程如表(单位:km):
(1)该车最后是否回到了车站?为什么?
(2)该车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若每行驶1km耗油0.06升,求出该车在上述过程中共耗油多少升?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)该车离开出发点最远是多少千米?
(3)这辆车在上述过程中一共行驶了多少路程?
(4)若每行驶1km耗油0.06升,求出该车在上述过程中共耗油多少升?
15.实数$\sqrt{2}$-1的相反数是( )
| A. | $\sqrt{2}$+1 | B. | -$\sqrt{2}$+1 | C. | -$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |

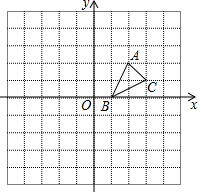 如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).
如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1). 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.