题目内容
 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.| A、4.2 | B、4 |
| C、3.8 | D、3.5 |
考点:反比例函数的应用
专题:
分析:首先求的反比例函数的解析式,然后将0.45代入即可求的相关数据.
解答:解:设反比例函数的解析式为y=
.
∵由图象知经过点(12,9)
∴k=12×9=108
∴解析式为:y=
(x>12)
令y=0.45得:x=108÷0.45=240分钟=4小时,
则从药物释放完毕开始需要:4-
=3.8小时,学生才能进入教室.
故选C.
| k |
| x |
∵由图象知经过点(12,9)
∴k=12×9=108
∴解析式为:y=
| 108 |
| x |
令y=0.45得:x=108÷0.45=240分钟=4小时,
则从药物释放完毕开始需要:4-
| 12 |
| 60 |
故选C.
点评:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
+|3x-2y-a|=0,y为负数,则a的取值范围为( )
| x-2 |
| A、a≥2 | B、a<3 |
| C、a>6 | D、a≥5 |
已知
=
,
=
,
=
,则
=( )
| xy |
| x+y |
| 1 |
| 3 |
| yz |
| y+z |
| 1 |
| 5 |
| zx |
| z+x |
| 1 |
| 6 |
| xyz |
| xy+yz+zx |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )
如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40°,则∠ADB的度数是( )| A、50° | B、60° |
| C、70° | D、80° |
下列各式:①(
)-2=9;②(-2)0=1;③(a+b)2=a2+b2;④(-3ab3)2=9a2b6;⑤
-
=2,其中计算正确的是( )
| 1 |
| 3 |
| 12 |
| 3 |
| A、①②③ | B、①②④ |
| C、③④⑤ | D、②④⑤ |
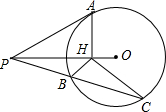 如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算
如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算 已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想.
已知直角三角形ABC中,∠C=90°,AC=a,BC=2a.在AC、BC上分别有一动点P、Q,且PQ始终平分△ABC的面积.作PR⊥CA交AB于R,QS⊥BC交AB于S.线段BS、SR、RA能否构成一个直角三角形,证明你的猜想. 如图,直线AD对应的函数关系式为y=-x-1,与抛物线交于点A(在x轴上)、点D,抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,-3),
如图,直线AD对应的函数关系式为y=-x-1,与抛物线交于点A(在x轴上)、点D,抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,-3), 已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值.
已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值.