题目内容
 已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值.
已知二次函数y=ax2+(a2-3a-4)x-12a的图象关于y轴对称,并有最大值.(1)求此二次函数的解析式,并画出图象.
(2)若此二次函数与x轴交于点A、B,△ABC为等边三角形(点C在x轴上方),求点C的坐标.
(3)在此二次函数图象上是否存在点P,使∠APB=60°?若有,请求出点P的坐标;若没有,请说明理由.
考点:二次函数综合题
专题:代数几何综合题
分析:(1)根据抛物线对称轴为y轴列式求解得到a的值,然后代入抛物线计算即可得解,然后画出图象即可;
(2)先求出AB的长度,再根据△ABC是等边三角形利用等边三角形的性质可得点C一定在AB的中垂线上,即点C在y轴上,然后根据等边三角形的性质求出AB边上的高,写出点C的坐标即可;
(3)根据在同圆或等圆中,同弧所对的圆周角相等,作△ABC的外接圆,然后写出圆的解析式,再与抛物线解析式联立求解即可得到点P的坐标,再根据对称性写出关于x轴对称的圆的解析式,再与抛物线解析式联立求解即可得到点P的坐标,综合以上两种情况即可得解.
(2)先求出AB的长度,再根据△ABC是等边三角形利用等边三角形的性质可得点C一定在AB的中垂线上,即点C在y轴上,然后根据等边三角形的性质求出AB边上的高,写出点C的坐标即可;
(3)根据在同圆或等圆中,同弧所对的圆周角相等,作△ABC的外接圆,然后写出圆的解析式,再与抛物线解析式联立求解即可得到点P的坐标,再根据对称性写出关于x轴对称的圆的解析式,再与抛物线解析式联立求解即可得到点P的坐标,综合以上两种情况即可得解.
解答: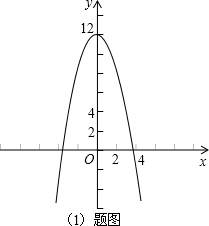 解:(1)∵二次函数的对称轴为y轴,
解:(1)∵二次函数的对称轴为y轴,
∴-
=0,
解得,a=4或-1,
又∵二次函数有最大值,
∴a=-1,
∴二次函数解析式为,y=-x2+12,
函数图象如右图所示;
(2)令y=0,则-x2+12=0,
解得x=±2
,
∴AB=2
-(-2
)=2
+2
=4
,
∵△ABC是等边三角形,且AO=BO,
∴点C一定在AB的中垂线上,即点C在y轴上,
所以,点C到AB的距离为,4
×sin60°=4
×
=6,
∵点C在x轴上方,
∴点C的坐标为(0,6);
(3)存在.理由如下:
如图,∵∠APB=60°,
∴作△ABC的外接圆,则圆心坐标为(0,2),
 则圆的解析式为x2+(y-2)2=(6-2)2,
则圆的解析式为x2+(y-2)2=(6-2)2,
又∵点P在抛物线图象上,
∴12-y+(y-2)2=16,
整理得,y2-5y=0,
解得y1=0(舍去),y2=5,
此时,-x2+12=5,
解得x=±
,
所以,点P的坐标为(
,5)或(-
,5),
根据对称性,当圆心在(0,-2)时,
则圆的解析式为x2+(y+2)2=(6-2)2,
又∵点P在抛物线图象上,
∴12-y+(y+2)2=16,
整理得,y2+3y=0,
解得y1=0(舍去),y2=-3,
此时,-x2+12=-3,
解得,x=±
,
所以,点P的坐标为(
,-3)或(-
,-3),
综上所述,二次函数图象上存在点P(
,5)或(-
,5)或(
,-3)或(-
,-3)使∠APB=60°.
 解:(1)∵二次函数的对称轴为y轴,
解:(1)∵二次函数的对称轴为y轴,∴-
| a2-3a-4 |
| 2a |
解得,a=4或-1,
又∵二次函数有最大值,
∴a=-1,
∴二次函数解析式为,y=-x2+12,
函数图象如右图所示;
(2)令y=0,则-x2+12=0,
解得x=±2
| 3 |
∴AB=2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∵△ABC是等边三角形,且AO=BO,
∴点C一定在AB的中垂线上,即点C在y轴上,
所以,点C到AB的距离为,4
| 3 |
| 3 |
| ||
| 2 |
∵点C在x轴上方,
∴点C的坐标为(0,6);
(3)存在.理由如下:
如图,∵∠APB=60°,
∴作△ABC的外接圆,则圆心坐标为(0,2),
 则圆的解析式为x2+(y-2)2=(6-2)2,
则圆的解析式为x2+(y-2)2=(6-2)2,又∵点P在抛物线图象上,
∴12-y+(y-2)2=16,
整理得,y2-5y=0,
解得y1=0(舍去),y2=5,
此时,-x2+12=5,
解得x=±
| 7 |
所以,点P的坐标为(
| 7 |
| 7 |
根据对称性,当圆心在(0,-2)时,
则圆的解析式为x2+(y+2)2=(6-2)2,
又∵点P在抛物线图象上,
∴12-y+(y+2)2=16,
整理得,y2+3y=0,
解得y1=0(舍去),y2=-3,
此时,-x2+12=-3,
解得,x=±
| 15 |
所以,点P的坐标为(
| 15 |
| 15 |
综上所述,二次函数图象上存在点P(
| 7 |
| 7 |
| 15 |
| 15 |
点评:本题是对二次函数的综合考查,主要利用了二次函数的对称性,等边三角形的性质,在同圆或等圆中,同弧所对的圆周角相等的性质,(3)利用圆的解析式与抛物线的解析式联立求解是解题的关键.

练习册系列答案
相关题目
下列多项式不能用平方差公式分解因式的是( )
| A、a2-b2 |
| B、16a2-b2 |
| C、-a2+25b2 |
| D、-4-a2 |
 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.| A、4.2 | B、4 |
| C、3.8 | D、3.5 |
若不等式组
有解,则实数a的取值范围为( )
|
A、a≤
| ||
B、a<
| ||
C、a≥
| ||
D、a>
|

 如图,已知正五边形ABCDE中,BF与CM相交于点P,CF=DM.
如图,已知正五边形ABCDE中,BF与CM相交于点P,CF=DM.