题目内容
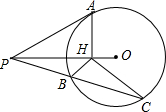 如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算
如图,已知PA切⊙O于A,∠APO=30°,AH⊥PO于H,任作割线PBC交⊙O于点B、C,计算| HC-HB |
| BC |
考点:圆的综合题
专题:综合题
分析:连OB、OC、OA,根据切线的性质得到OA⊥PA,即∠PAO=90°,易证得Rt△PAH∽Rt△POA,则PA:PO=PH:PA,即PA2=PH•PO,由切割线定理得PA2=PB•PC,则有PH•PO=PB•PC,根据三角形相似的判定得到△PBH∽△POC,则∠PBH=∠POC,
=
,即
=
①,根据四点共圆的判定方法得到点H、B、C、O四点共圆,利用在同圆或等圆中同弧所对的圆周角相等得到∠HOB=∠HCB,易证得△PBO∽△PHC,于是有
=
,即
=
②,由①②得
=
,即
=
,利用比例的性质得到
=
=
,则有
=
,由①得
=
=
,在Rt△OAP中,∠APO=30°,则OP=2OA,即可得到
的值.
| BH |
| OC |
| PB |
| PO |
| BH |
| PB |
| OC |
| PO |
| OB |
| HC |
| PO |
| PC |
| OB |
| PO |
| HC |
| PC |
| BH |
| PB |
| HC |
| PC |
| HC |
| BH |
| PC |
| PB |
| HC-BH |
| BH |
| PC-PB |
| PB |
| BC |
| PB |
| HC-HB |
| BC |
| BH |
| PB |
| HC-HB |
| BC |
| OC |
| PO |
| OA |
| OP |
| HC-HB |
| BC |
解答:解:连接OB、OC、OA,如图,
∵PA为⊙O的切线,
∴OA⊥PA,即∠PAO=90°,
而AH⊥OP,
∴∠PHA=90°,
∴Rt△PAH∽Rt△POA,
∴PA:PO=PH:PA,即PA2=PH•PO,
又∵PBC为⊙O的割线,
∴PA2=PB•PC,
∴PH•PO=PB•PC,
∴△PBH∽△POC,
∴∠PBH=∠POC,
=
,即
=
①,
∴点H、B、C、O四点共圆,
∴∠HOB=∠HCB,
∴△PBO∽△PHC,
∴
=
,即
=
②,
由①②得
=
,即
=
,
∴
=
=
,
∴
=
,
∴
=
=
,
∵在Rt△OAP中,∠APO=30°,则OP=2OA,
∴
=
.

∵PA为⊙O的切线,
∴OA⊥PA,即∠PAO=90°,
而AH⊥OP,
∴∠PHA=90°,
∴Rt△PAH∽Rt△POA,
∴PA:PO=PH:PA,即PA2=PH•PO,
又∵PBC为⊙O的割线,
∴PA2=PB•PC,
∴PH•PO=PB•PC,
∴△PBH∽△POC,
∴∠PBH=∠POC,
| BH |
| OC |
| PB |
| PO |
| BH |
| PB |
| OC |
| PO |
∴点H、B、C、O四点共圆,
∴∠HOB=∠HCB,
∴△PBO∽△PHC,
∴
| OB |
| HC |
| PO |
| PC |
| OB |
| PO |
| HC |
| PC |
由①②得
| BH |
| PB |
| HC |
| PC |
| HC |
| BH |
| PC |
| PB |
∴
| HC-BH |
| BH |
| PC-PB |
| PB |
| BC |
| PB |
∴
| HC-HB |
| BC |
| BH |
| PB |
∴
| HC-HB |
| BC |
| OC |
| PO |
| OA |
| OP |
∵在Rt△OAP中,∠APO=30°,则OP=2OA,
∴
| HC-HB |
| BC |
| 1 |
| 2 |
点评:本题考查了圆的综合题:圆的切线垂直于过切点的半径;四边形的对角互补,则四点在同一个圆上;在同圆或等圆中同弧所对的圆周角相等;利用相似三角形的判定与性质证明比例线段,运用比例的性质以及含30度的直角三角形三边的关系进行几何计算.

练习册系列答案
相关题目
一幅地图的比例尺为1:10000,经测量得某地方在地图上的面积为10cm2,则该地方的实际面积为( )
| A、100m2 |
| B、1000m2 |
| C、10000m2 |
| D、100000m2 |
下列多项式不能用平方差公式分解因式的是( )
| A、a2-b2 |
| B、16a2-b2 |
| C、-a2+25b2 |
| D、-4-a2 |
 在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.
在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.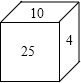 如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?
如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是? 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.