题目内容
已知
+|3x-2y-a|=0,y为负数,则a的取值范围为( )
| x-2 |
| A、a≥2 | B、a<3 |
| C、a>6 | D、a≥5 |
考点:非负数的性质:算术平方根,非负数的性质:绝对值
专题:计算题
分析:由二次根式和绝对值的非负数性质得到
=0且|3x-2y-a|=0,则x=2,3x-2y-a=0,可得到y=
,而y为负数,则有
<0,然后解不等式即可.
| x-2 |
| 6-a |
| 2 |
| 6-a |
| 2 |
解答:解:∵
+|3x-2y-a|=0,
∴
=0且|3x-2y-a|=0,
∴x-2=0且3x-2y-a=0,
∴6-2y-a=0,
∴y=
而y为负数,
∴
<0,
∴a>6.
故选C.
| x-2 |
∴
| x-2 |
∴x-2=0且3x-2y-a=0,
∴6-2y-a=0,
∴y=
| 6-a |
| 2 |
而y为负数,
∴
| 6-a |
| 2 |
∴a>6.
故选C.
点评:本题考查了二次根式的性质:
≥0(a≥0).也考查了绝对值的非负数性质.
| a |

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、为检测我市正在销售的酸奶质量,应该采用抽样调查的方式 | ||
| B、两名同学连续五次数学测试的平均分相同,方差较大的同学数学成绩更稳定 | ||
C、抛掷一个正方体骰子,点数为奇数的概率是
| ||
| D、“打开电视,正在播放广告”是必然事件 |
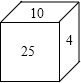 如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?
如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?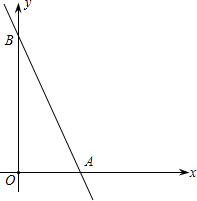 已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2.
已知直线y=-2x+6交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B两点及x轴上另一点C,且AC=2. 为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.
为了预防流感,某中学在周末用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物释放完毕后y与x成反比例;整个过程中y与x的图象如右图,据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放完毕开始至少需经过( )小时,学生才能进入教室.