题目内容
11.下列各组条件中,可保证△ABC与△A′B′C′全等的是( )| A. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | B. | AB=A′B′,AC=A′C′,∠B=∠B′ | ||
| C. | AB=C′B′,∠A=∠B′,∠C=∠C′ | D. | CB=A′B′,AC=A′C′,BA=B′C′ |
分析 要判断可否保证△ABC与△A′B′C′全等,主要验证各选项提供的已知条件能否符合全等三角形的判定方法,符合的是正确的,如选项D提供的条件符合SSS,于是可得答案.
解答 解:A选项,给出的条件为AAA,因此不能确定两三角形全等;
B选项,给出的条件为SSA,因此也不能确定两三角形全等;
C选项,给出的条件为AAS与ASA,因此也不能确定两三角形全等;
D选项,给出的条件为SSS,符合全等三角形的判定定理,因此能确定;
故选D.
点评 本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.

练习册系列答案
相关题目
1.如果|x+1|=1+x,|3x+2|=-3x-2,那么x的取值范围是( )
| A. | -1$≤x≤-\frac{2}{3}$ | B. | x≥-1 | C. | x$≤-\frac{2}{3}$ | D. | $-\frac{2}{3}≤x≤-1$ |
19.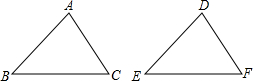 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
 如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )
如图,在△ABC和△DEF中,∠B=∠E,∠C=∠F,若要使△ABC≌△DEF,则可添加的条件为( )| A. | BC=EF | B. | AB=DF | C. | AC=DE | D. | ∠A=∠D |
16.若a为方程x2+2x-5=0的解,则3a2+6a+1的值为( )
| A. | 12 | B. | 16 | C. | 9 | D. | 6 |
 一张圆桌旁有四个座位,A先坐在如图所示的位置上,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而座的概率为$\frac{1}{3}$.
一张圆桌旁有四个座位,A先坐在如图所示的位置上,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而座的概率为$\frac{1}{3}$.