题目内容
3.已知$\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=k$(a+b+c≠0),那么函数y=kx+k的图象一定不经过第四象限.分析 利用比例的等比性质正确求得k的值,然后根据直线解析式中的k,b的值正确判断直线经过的象限.
解答 解:当a+b+c≠0时,根据比例的等比性质,得k=$\frac{2(a+b+c)}{a+b+c}$=2,
则直线解析式是y=2x+2,
则图象一定经过一、二、三象限.
故答案为:四.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b>0时,函数的图象在一、二、三象限是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13.一元二次方程3x2-7x-12=0的二次项、一次项和常数项分别是( )
| A. | 3x2,7x,12 | B. | 3x2,-7x,12 | C. | 3x2,7x,-12 | D. | 3x2,-7x,-12 |
14.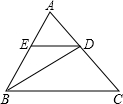 如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
 如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )
如图,△ABC中,BD是∠ABC的角平分线,DE∥BC,交AB于E,∠A=60°,∠BDC=95°,则∠BED的度数是( )| A. | 35° | B. | 70° | C. | 110° | D. | 130° |
11.下列各组条件中,可保证△ABC与△A′B′C′全等的是( )
| A. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | B. | AB=A′B′,AC=A′C′,∠B=∠B′ | ||
| C. | AB=C′B′,∠A=∠B′,∠C=∠C′ | D. | CB=A′B′,AC=A′C′,BA=B′C′ |
 已知:如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.若要证明BD=CE,则只要证明△BDC≌△CEB.
已知:如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.若要证明BD=CE,则只要证明△BDC≌△CEB.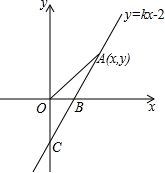 如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC=$\frac{1}{2}$.
如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC=$\frac{1}{2}$.