题目内容
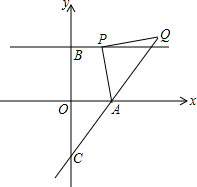 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.(1)当a=1时,则点Q的坐标为
(2)当点P在直线上运动时,点Q也随之运动.当a=
考点:一次函数综合题,全等三角形的判定与性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)要求点Q的坐标,可作QF⊥BP,由于BP、OB已知,只需求出PF和QF.从条件“△APQ为等腰直角三角形”出发,构造全等,即可解决问题.
(2)本题要求动点Q到两定点A、B的距离之和AQ+BQ的最小值,属于“将军饮马型”,只需求出动点Q所在直线的解析式,然后运用解决“将军饮马型”的方法即可解决问题;要求AQ+BQ取最小值时对应的a的值,只需运用相似三角形对应高的比等于相似比建立关于a的方程,就可求出a的值.
(2)本题要求动点Q到两定点A、B的距离之和AQ+BQ的最小值,属于“将军饮马型”,只需求出动点Q所在直线的解析式,然后运用解决“将军饮马型”的方法即可解决问题;要求AQ+BQ取最小值时对应的a的值,只需运用相似三角形对应高的比等于相似比建立关于a的方程,就可求出a的值.
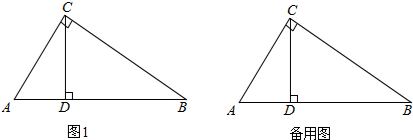
解答:解:(1)过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F,如图1.
∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°.
∵∠APQ=90°,∴∠EPA=∠FPQ=90°-∠APF.
在△PEA和△PFQ中,
∴△PEA≌△PFQ.
∴PE=PF,EA=QF.
∵a=1,∴P(1,3).∴OE=BP=1,PE=3.
∵A(2,0),∴OA=2,∴EA=1.∴PF=3,QF=1.
∴点Q的坐标为(4,4).
(2)若点P的坐标为(a,3),则PF=PE=3,QF=AE=|2-a|.
∴点Q的坐标为(a+3,5-a).
∵无论a为何值,点Q的坐标(a+3,5-a)都满足一次函数解析式y=-x+8,
∴点Q始终在直线y=-x+8上运动.
设直线y=-x+8与x轴、y轴分别交于点M、N,如图2所示.
当x=0时y=8,当y=0时x=8.∴OM=ON=8.
∵∠AOB=90°,∴∠OMN=45°.
过点A关于直线MN作对称点A′,连A′Q、A′M,
则A′Q=AQ,A′M=AM=6,∠A′MN=∠AMN=45°.
∴∠A′MA=90°,AQ+BQ=A′Q+BQ.根据两点之间线段最短可知:
当A′、Q、B三点共线时,AQ+BQ=A′Q+BQ最短,最小值为A′B长.
设直线BP与A′M相交于点H,则BH⊥A′M.
在Rt△A′HB=90°,BH=OM=8,A′H=A′M-MH=6-3=3,
∴A′B=
=
=
.
当A′、Q、B三点共线时,
∵BN∥A′M,∴△BQN~△A′QM.
根据相似三角形对应高的比等于相似比可得:
=
=
,解得xQ=
.
∴a+3=
.∴a=
.
∴当a=
时,AQ+BQ的值最小为
.
故答案为:(4,4)、
、
.
∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°.

∵∠APQ=90°,∴∠EPA=∠FPQ=90°-∠APF.
在△PEA和△PFQ中,
|
∴△PEA≌△PFQ.
∴PE=PF,EA=QF.
∵a=1,∴P(1,3).∴OE=BP=1,PE=3.
∵A(2,0),∴OA=2,∴EA=1.∴PF=3,QF=1.
∴点Q的坐标为(4,4).
(2)若点P的坐标为(a,3),则PF=PE=3,QF=AE=|2-a|.
∴点Q的坐标为(a+3,5-a).
∵无论a为何值,点Q的坐标(a+3,5-a)都满足一次函数解析式y=-x+8,
∴点Q始终在直线y=-x+8上运动.
设直线y=-x+8与x轴、y轴分别交于点M、N,如图2所示.

当x=0时y=8,当y=0时x=8.∴OM=ON=8.
∵∠AOB=90°,∴∠OMN=45°.
过点A关于直线MN作对称点A′,连A′Q、A′M,
则A′Q=AQ,A′M=AM=6,∠A′MN=∠AMN=45°.
∴∠A′MA=90°,AQ+BQ=A′Q+BQ.根据两点之间线段最短可知:
当A′、Q、B三点共线时,AQ+BQ=A′Q+BQ最短,最小值为A′B长.
设直线BP与A′M相交于点H,则BH⊥A′M.
在Rt△A′HB=90°,BH=OM=8,A′H=A′M-MH=6-3=3,
∴A′B=
| BH2+A′H2 |
| 82+32 |
| 73 |
当A′、Q、B三点共线时,
∵BN∥A′M,∴△BQN~△A′QM.
根据相似三角形对应高的比等于相似比可得:
| xQ |
| 8-xQ |
| BN |
| A′M |
| 8-3 |
| 6 |
| 40 |
| 11 |
∴a+3=
| 40 |
| 11 |
| 7 |
| 11 |
∴当a=
| 7 |
| 11 |
| 73 |
故答案为:(4,4)、
| 7 |
| 11 |
| 73 |
点评:这道题考查了全等的性质与判定、相似的性质与判定,两点之间线段最短,勾股定理等知识,综合性很强,求出动点Q所在直线的解析式是解决这道难题的关键;当直角坐标系中出现等腰直角三角形时,可考虑构造全等三角形,找出线段之间的等量关系,从而将条件与所求线段有机地联系起来;若要求一个动点到两个定点的距离之和的最小值,应联想到“将军饮马”这个基本模型.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA=
在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA=

 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,
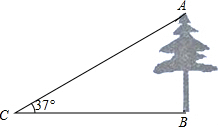 如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.
如图,在一次数学课外实践活动,小文在点C处测得树的顶端A的仰角为37°,BC=20m,求树的高度AB.