题目内容
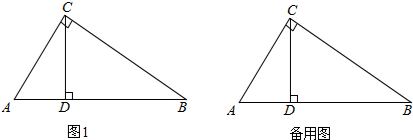
如图1,在△ABC中,∠C=90°,AC=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.
(1)求线段AD的长;
(2)若EF⊥AB,当点E在斜边AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围);
②当x取何值时,y有最大值?并求出最大值.
(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.

(1)求线段AD的长;
(2)若EF⊥AB,当点E在斜边AB上移动时,
①求y与x的函数关系式(写出自变量x的取值范围);
②当x取何值时,y有最大值?并求出最大值.
(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.
考点:二次函数综合题
专题:
分析:(1)先根据勾股定理求出AB的长,再根据Rt△ADC∽Rt△ACB,利用其相似比即可求出AD的长;
(2)①分别根据x的取值范围及三角形的面积公式分类可得x、y的函数关系式;
②根据①中所求的函数关系式求出其最值即可.
(3)先求得△ABC的面积的
,进而得到△AEF得到面积的函数关系式,让它等于3列式即可求解.
(2)①分别根据x的取值范围及三角形的面积公式分类可得x、y的函数关系式;
②根据①中所求的函数关系式求出其最值即可.
(3)先求得△ABC的面积的
| 1 |
| 2 |
解答:解:(1)∵△ABC中,∠C=90°,AC=3,BC=4,
∴AB=
=5,
∵CD⊥AB,
∴∠CDA=∠ACB,
又∠CAD=∠CAD,
∴Rt△ADC∽Rt△ACB,
∴
=
,即
=
,AD=
.
(2)①由于E的位置不能确定,故应分两种情况讨论:
如图A:当0<x≤AD,即0<x≤
时,
∵EF⊥AB,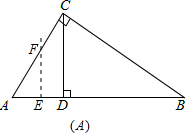
∴Rt△AEF∽Rt△ACB,即
=
,
∵AC=3,BC=4,AE=x,
∴
=
,EF=
x,
S△AEF=y=
AE•EF=
x•
x=
x2.
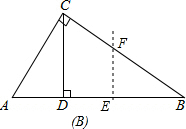
如图B:当AD<x≤AB,即
<x≤5时,
∵EF⊥AB,
∴Rt△BEF∽Rt△BCA,
∴
=
,
∵AE=x,△AEF的面积为y,
=
,
∴EF=
,
y=
×AE×EF=
x•
=
-
.
②当如图A:当0<x≤AD,即0<x≤
时,
S△AEF=y=
AE•EF=
x•
x=
x2,当x=AD,即x=
时,y最大=
×(
)2=
.
如图B:当AD<x≤BD,即
<x≤5时,
y=
x×
(5-x)=
-
,y最大=
,此时x=2.5<5,故成立.
故y最大=
.
(3)存在.
假设存在,当0<x≤5时,AF=6-x,∴0<6-x<3,
∴3<x<6,
∴3<x≤5,
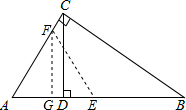
作FG⊥AB于点G,
由△AFG∽△ACD,
∴
=
,
∴
=
,
即FG=
(6-x),
∴S△AEF=
x•
(6-x)=-
x2+
x,
∴3=-
x2+
x,
解得:x1=
,x2=
,
∵3<x≤5,
∴x1=
(符合题意),x2=
(不合题意,应舍去),
故存在x,直线EF将△ABC的周长和面积同时平分,此时x=
.
∴AB=
| 32+42 |
∵CD⊥AB,
∴∠CDA=∠ACB,
又∠CAD=∠CAD,
∴Rt△ADC∽Rt△ACB,
∴
| AD |
| AC |
| AC |
| AB |
| AD |
| 3 |
| 3 |
| 5 |
| 9 |
| 5 |
(2)①由于E的位置不能确定,故应分两种情况讨论:
如图A:当0<x≤AD,即0<x≤
| 9 |
| 5 |
∵EF⊥AB,

∴Rt△AEF∽Rt△ACB,即
| AE |
| AC |
| EF |
| BC |
∵AC=3,BC=4,AE=x,
∴
| x |
| 3 |
| EF |
| 4 |
| 4 |
| 3 |
S△AEF=y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
如图B:当AD<x≤AB,即
| 9 |
| 5 |
∵EF⊥AB,
∴Rt△BEF∽Rt△BCA,
∴
| EB |
| BC |
| EF |
| AC |
∵AE=x,△AEF的面积为y,
| 5-x |
| 4 |
| EF |
| 3 |
∴EF=
| 15-3x |
| 4 |

y=
| 1 |
| 2 |
| 1 |
| 2 |
| 15-3x |
| 4 |
| 15x |
| 8 |
| 3x2 |
| 8 |
②当如图A:当0<x≤AD,即0<x≤
| 9 |
| 5 |
S△AEF=y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 9 |
| 5 |
| 2 |
| 3 |
| 9 |
| 5 |
| 54 |
| 25 |
如图B:当AD<x≤BD,即
| 9 |
| 5 |
y=
| 1 |
| 2 |
| 3 |
| 4 |
| 15x |
| 8 |
| 3x2 |
| 8 |
| 75 |
| 32 |
故y最大=
| 75 |
| 32 |
(3)存在.
假设存在,当0<x≤5时,AF=6-x,∴0<6-x<3,
∴3<x<6,
∴3<x≤5,
作FG⊥AB于点G,
由△AFG∽△ACD,
∴
| AF |
| AC |
| FG |
| CD |

∴
| 6-x |
| 3 |
| FG | ||
|
即FG=
| 4 |
| 5 |
∴S△AEF=
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 12 |
| 5 |
∴3=-
| 2 |
| 5 |
| 12 |
| 5 |
解得:x1=
6+
| ||
| 2 |
6-
| ||
| 2 |
∵3<x≤5,
∴x1=
6+
| ||
| 2 |
6-
| ||
| 2 |
故存在x,直线EF将△ABC的周长和面积同时平分,此时x=
6+
| ||
| 2 |
点评:此题考查了二次函数的综合知识,比较复杂,是典型的动点问题,涉及面较广,涉及到勾股定理、二次函数的最值及相似三角形的有关知识,综合性较强.

练习册系列答案
相关题目
 如图,∠AOB=45°,点O1在OA上,OO1=7,⊙O1的半径为2,点O2在射线OB上运动,且⊙O2始终与OA相切,当⊙O2和⊙O1相切时,⊙O2的半径等于
如图,∠AOB=45°,点O1在OA上,OO1=7,⊙O1的半径为2,点O2在射线OB上运动,且⊙O2始终与OA相切,当⊙O2和⊙O1相切时,⊙O2的半径等于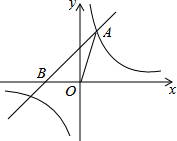 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
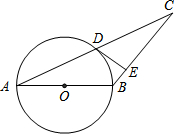 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E.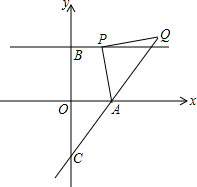 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.