题目内容
木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
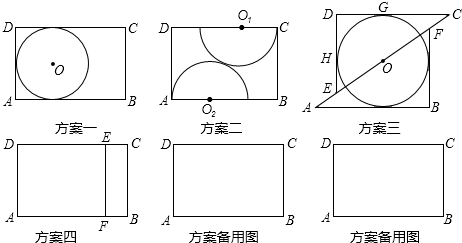
方案一:直接锯一个半径最大的圆;
方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.
(1)写出方案一中圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.
方案一:直接锯一个半径最大的圆;
方案二:圆心O1、O2分别在CD、AB上,半径分别是O1C、O2A,锯两个外切的半圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼到矩形AFED下面,利用拼成的木板锯一个尽可能大的圆.
(1)写出方案一中圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE=x(0<x<1),圆的半径为y.
①求y关于x的函数解析式;
②当x取何值时圆的半径最大,最大半径为多少?并说明四种方案中哪一个圆形桌面的半径最大.

考点:圆的综合题
专题:压轴题
分析:(1)观察图易知,截圆的直径需不超过长方形长、宽中最短的边,由已知长宽分别为3,2,那么直接取圆直径最大为2,则半径最大为1.
(2)方案二、方案三中求圆的半径是常规的利用勾股定理或三角形相似中对应边长成比例等性质解直角三角形求边长的题目.一般都先设出所求边长,而后利用关系代入表示其他相关边长,方案二中可利用△O1O2E为直角三角形,则满足勾股定理整理方程,方案三可利用△AOM∽△OFN后对应边成比例整理方程,进而可求r的值.
(3)①类似(1)截圆的直径需不超过长方形长、宽中最短的边,虽然方案四中新拼的图象不一定为矩形,但直径也不得超过横纵向方向跨度.则选择最小跨度,取其
,即为半径.由EC为x,则新拼图形水平方向跨度为3-x,竖直方向跨度为2+x,则需要先判断大小,而后分别讨论结论.
②已有关系表达式,则直接根据不等式性质易得方案四中的最大半径.另与前三方案比较,即得最终结论.
(2)方案二、方案三中求圆的半径是常规的利用勾股定理或三角形相似中对应边长成比例等性质解直角三角形求边长的题目.一般都先设出所求边长,而后利用关系代入表示其他相关边长,方案二中可利用△O1O2E为直角三角形,则满足勾股定理整理方程,方案三可利用△AOM∽△OFN后对应边成比例整理方程,进而可求r的值.
(3)①类似(1)截圆的直径需不超过长方形长、宽中最短的边,虽然方案四中新拼的图象不一定为矩形,但直径也不得超过横纵向方向跨度.则选择最小跨度,取其
| 1 |
| 2 |
②已有关系表达式,则直接根据不等式性质易得方案四中的最大半径.另与前三方案比较,即得最终结论.
解答:解:(1)方案一中的最大半径为1.
分析如下:
因为长方形的长宽分别为3,2,那么直接取圆直径最大为2,则半径最大为1;
(2)如图1,方案二中连接O1,O2,过O1作O1E⊥AB于E,方案三中,过点O分别作AB,BF的垂线,交于M,N,此时M,N恰为⊙O与AB,BF的切点.

方案二:
设半径为r,
在Rt△O1O2E中,
∵O1O2=2r,O1E=BC=2,O2E=AB-AO2-CO1=3-2r,
∴(2r)2=22+(3-2r)2,
解得 r=
.
方案三:
设半径为r,
在△AOM和△OFN中,
,
∴△AOM∽△OFN,
∴
=
,
∴
=
,
解得 r=
.
比较知,方案三半径较大;
(3)
①∵EC=x,
∴新拼图形水平方向跨度为3-x,竖直方向跨度为2+x.
类似(1),所截出圆的直径最大为3-x或2+x较小的.
a.当3-x<2+x时,即当1>x>
时,y=
(3-x);
b.当3-x=2+x时,即当x=
时,y=
(3-
)=
;
c.当3-x>2+x时,即当0<x<
时,y=
(2+x).
②当x>
时,y=
(3-x)<
(3-
)=
;
当x=
时,y=
(3-
)=
;
当x<
时,y=
(2+x)<
(2+
)=
,
∴方案四中,当x=
时,y最大为
.
∵1<
<
<
,
∴方案四时可取的圆桌面积最大.
分析如下:
因为长方形的长宽分别为3,2,那么直接取圆直径最大为2,则半径最大为1;
(2)如图1,方案二中连接O1,O2,过O1作O1E⊥AB于E,方案三中,过点O分别作AB,BF的垂线,交于M,N,此时M,N恰为⊙O与AB,BF的切点.

方案二:
设半径为r,
在Rt△O1O2E中,
∵O1O2=2r,O1E=BC=2,O2E=AB-AO2-CO1=3-2r,
∴(2r)2=22+(3-2r)2,
解得 r=
| 13 |
| 12 |
方案三:
设半径为r,
在△AOM和△OFN中,
|
∴△AOM∽△OFN,
∴
| OM |
| AM |
| FN |
| ON |
∴
| r |
| 3-r |
| 2-r |
| r |
解得 r=
| 6 |
| 5 |
比较知,方案三半径较大;
(3)
①∵EC=x,
∴新拼图形水平方向跨度为3-x,竖直方向跨度为2+x.
类似(1),所截出圆的直径最大为3-x或2+x较小的.
a.当3-x<2+x时,即当1>x>
| 1 |
| 2 |
| 1 |
| 2 |
b.当3-x=2+x时,即当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
c.当3-x>2+x时,即当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
②当x>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
当x<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
∴方案四中,当x=
| 1 |
| 2 |
| 5 |
| 4 |
∵1<
| 13 |
| 12 |
| 6 |
| 5 |
| 5 |
| 4 |
∴方案四时可取的圆桌面积最大.
点评:本题考查了圆的基本性质及通过勾股定理、三角形相似等性质求解边长及分段函数的表示与性质讨论等内容,题目虽看似新颖不易找到思路,但仔细观察每一小问都是常规的基础考点,所以总体来说是一道质量很高的题目,值得认真练习.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 由六个相同的正方体搭成的几何体如图,则它的主视图是( )
由六个相同的正方体搭成的几何体如图,则它的主视图是( )A、 |
B、 |
C、 |
D、 |
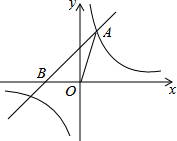 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=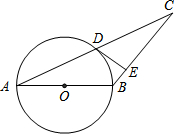 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E. 如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43) 如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)
如图,某校数学学习兴趣小组为测量学校旗杆AB的高度,测得教学楼一楼底部C处与旗杆底部B处的水平距离为5米,旗杆底部与教学楼一楼在同一水平线上,在教学楼三楼底部D处测得旗杆顶部A的仰角为27°.若CD的高度为6米,请你帮助该小组计算旗杆AB的高(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.51)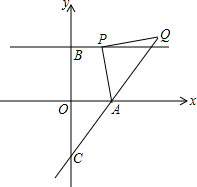 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.