题目内容
 在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA=6
在平面直角坐标系xOy中,点A在第一象限,点B(30,0),OA=6| 3 |
| 3 |
| 3 |
| 3 |
(1)填空:A、M、N三点坐标分别为
A(
(2)用t的代数式表示y.
(3)在运动过程时,⊙M与⊙N相切,求t的值.
(4)在运动的过程中,是否存在这样的时刻t,使得△OMN是等腰三角形?若存在,求出t的所有可能值;若不存在,说明理由.
考点:圆的综合题
专题:
分析:(1)求A、M、N点坐标,需要分别表示出其横纵坐标,故过A、M作x轴的垂线,由已知∠AOB=30°,则利用含30°直角三角形边长性质易得结果.
(2)y=MN2,由MN即为M、N点之间距离,通常作关于x轴、y轴直线,再利用直角三角形中勾股定理求解斜边的长,由坐标易得此直角三角形另外两直角边的长,所以易得y与t的关系式,注意还要讨论t的取值范围.
(3)两圆相切,即有内切、外切三种情形,由已知rM>rN,则内切、外切共两种情形,即MN=rM+rN或MN=rM-rN.由(2)结论,易得方程,求解t即可.
(4)成等腰三角形,也有三种情形,OM=ON,或OM=MN,或MN=ON.有(1)、(2)结论,仿照(3)易得方程,求出所有t即可.
(2)y=MN2,由MN即为M、N点之间距离,通常作关于x轴、y轴直线,再利用直角三角形中勾股定理求解斜边的长,由坐标易得此直角三角形另外两直角边的长,所以易得y与t的关系式,注意还要讨论t的取值范围.
(3)两圆相切,即有内切、外切三种情形,由已知rM>rN,则内切、外切共两种情形,即MN=rM+rN或MN=rM-rN.由(2)结论,易得方程,求解t即可.
(4)成等腰三角形,也有三种情形,OM=ON,或OM=MN,或MN=ON.有(1)、(2)结论,仿照(3)易得方程,求出所有t即可.
解答:解:(1)A(9,3
),M(3t,
t),N(30-10t,0).
分析如下:

根据题意,如图1,过点A作AC⊥OB于C,过点M作MD⊥OB于D,
在Rt△OAC中,
∵∠AOB=30°,OA=6
,
∴AC=3
,OC=9,
∴A(9,3
).
在Rt△OMD中,
∵∠AOB=30°,OM=2
t,
∴MD=
t,OD=3t,
∴M(3t,
t).
∵OB=30,NB=10t,
∴ON=30-10t,
∴N(30-10t,0).
(2)
如图2,连接MN,
在Rt△MND中,
∵MD=
t,ND=ON-OD=30-10t-3t=30-13t,
∴MN2=MD2+ND2=(
t)2+(30-13t)2,
∴y=172t2-780t+900.
∵6
÷2
=3,30÷10=3,
∴y=172t2-780t+900(0≤t≤3).
(3)∵rM=3
+2.5,rN=3
-2.5,
∴rM>rN,
∵⊙M与⊙N相切,
∴MN=rM+rN=3
+2.5+(3
-2.5)=6
,
或MN=rM-rN=3
+2.5-(3
-2.5)=5,
①当MN=rM+rN时,
(6
)2=172t2-780t+900,解得 t=3 或t=
,
②当MN=rM-rN时,
25=172t2-780t+900,解得 t=
或t=2.5,
综上所述,t=
,
,2.5,3时,⊙M与⊙N相切.
(4)∵△OMN是等腰三角形,
∴OM=ON,或OM=MN,或MN=ON,
①当OM=ON时,
∵OM=2
t,ON=30-10t,
∴2
t=30-10t,
解得 t=
.
②当OM=MN时,
∵OM=2
t,MN2=172t2-780t+900,
∴(2
t)2=172t2-780t+900,
解得 t=
或t=3(此时,N运动至O点,不构成三角形舍去).
③当MN=ON时,
∵ON=30-10t,MN2=172t2-780t+900,
∴(30-10t)2=172t2-780t+900,
解得 t=0(此时,M在O点,不构成三角形舍去) 或t=2.5.
综上所述,t=
、
、2.5时,△OMN是等腰三角形.
| 3 |
| 3 |
分析如下:

根据题意,如图1,过点A作AC⊥OB于C,过点M作MD⊥OB于D,
在Rt△OAC中,
∵∠AOB=30°,OA=6
| 3 |
∴AC=3
| 3 |
∴A(9,3
| 3 |
在Rt△OMD中,
∵∠AOB=30°,OM=2
| 3 |
∴MD=
| 3 |
∴M(3t,
| 3 |
∵OB=30,NB=10t,
∴ON=30-10t,
∴N(30-10t,0).
(2)

如图2,连接MN,
在Rt△MND中,
∵MD=
| 3 |
∴MN2=MD2+ND2=(
| 3 |
∴y=172t2-780t+900.
∵6
| 3 |
| 3 |
∴y=172t2-780t+900(0≤t≤3).
(3)∵rM=3
| 3 |
| 3 |
∴rM>rN,
∵⊙M与⊙N相切,
∴MN=rM+rN=3
| 3 |
| 3 |
| 3 |
或MN=rM-rN=3
| 3 |
| 3 |
①当MN=rM+rN时,
(6
| 3 |
| 63 |
| 43 |
②当MN=rM-rN时,
25=172t2-780t+900,解得 t=
| 175 |
| 86 |
综上所述,t=
| 63 |
| 43 |
| 175 |
| 86 |
(4)∵△OMN是等腰三角形,
∴OM=ON,或OM=MN,或MN=ON,
①当OM=ON时,
∵OM=2
| 3 |
∴2
| 3 |
解得 t=
75-15
| ||
| 22 |
②当OM=MN时,
∵OM=2
| 3 |
∴(2
| 3 |
解得 t=
| 30 |
| 16 |
③当MN=ON时,
∵ON=30-10t,MN2=172t2-780t+900,
∴(30-10t)2=172t2-780t+900,
解得 t=0(此时,M在O点,不构成三角形舍去) 或t=2.5.
综上所述,t=
| 30 |
| 16 |
75-15
| ||
| 22 |
点评:本题考查了含30°角直角三角形特性、利用勾股定理表示坐标系中两点距离、动点构成圆的相切及构成等腰三角形时的基本情形.其考点及考法都非常常规,是一道非常值得学生练习基础的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
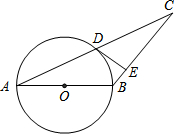 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DE⊥BC于点E. 如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
如图,已知墙高AB为6.5米,将一长为6米的梯子CD斜靠在墙面,梯子与地面所成的角∠BCD=55°,此时梯子的顶端与墙顶的距离AD为多少米?(结果精确到0.1米) (参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)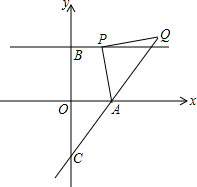 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.