题目内容
如图1,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.E(0,m)是线段OC上一动点(O,C点除外),直线EM交AB的延长线于点F.
(1)求点F的坐标(用含m的代数式表示);
(2)当△AEF是等腰三角形时,求m的值;
(3)如图2,以AE为直径作⊙P,求BC与⊙P恰好相切于点M时,求点F的坐标.

(1)求点F的坐标(用含m的代数式表示);
(2)当△AEF是等腰三角形时,求m的值;
(3)如图2,以AE为直径作⊙P,求BC与⊙P恰好相切于点M时,求点F的坐标.

考点:圆的综合题
专题:综合题
分析:(1)先证明△CEM≌△BFM,得到BF=CE,由于CE=OC-OE=2-m,所以BF=2-m,则AF=AB+BF=4-m,于是F点坐标表示为(2,4-m);
(2)先利用两点间的距离公式得到AF2=(4-m)2,AE2=22+m2,EF2=22+(4-2m)2,然后分类讨论:当AF=AE,则(4-m)2=22+m2;当AF=EF,(4-m)2=22+(4-2m)2,整理得3m2-8m+4=0;当AE=EF,22+m2=22+(4-2m)2,整理得3m2-16m+16=0,再分别解方程求出满足条件的m值(0<m<2);
(3)连结PM,根据切线的性质得PM⊥BC,易得PM为△EFA的中位线,则PM=
AF,而PM=
AE,所以AE=AF,然后利用(2)中的结论得当AF=AE,得m=
,所以F点的坐标为(2,
).
(2)先利用两点间的距离公式得到AF2=(4-m)2,AE2=22+m2,EF2=22+(4-2m)2,然后分类讨论:当AF=AE,则(4-m)2=22+m2;当AF=EF,(4-m)2=22+(4-2m)2,整理得3m2-8m+4=0;当AE=EF,22+m2=22+(4-2m)2,整理得3m2-16m+16=0,再分别解方程求出满足条件的m值(0<m<2);
(3)连结PM,根据切线的性质得PM⊥BC,易得PM为△EFA的中位线,则PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
解答:解: (1)∵正方形OABC的边长为2,M是BC的中点,
(1)∵正方形OABC的边长为2,M是BC的中点,
∴CM=CM=1,CO∥AB,
∴∠CEM=∠F,
在△CEM和△BFM中
,
∴△CEM≌△BFM,
∴BF=CE,
∵E点坐标为(0,m),
∴CE=OC-OE=2-m,
∴BF=2-m,
∴AF=AB+BF=4-m,
∴F点坐标为(2,4-m)(0<m<2);
(2)AF2=(4-m)2,AE2=22+m2,EF2=22+(4-2m)2,
当AF=AE,则(4-m)2=22+m2,解得m=
;
当AF=EF,(4-m)2=22+(4-2m)2,整理得3m2-8m+4=0,解得m1=
,m2=2(舍去);
当AE=EF,22+m2=22+(4-2m)2,整理得3m2-16m+16=0,解得m1=
,m2=4(舍去),
综上所述,当△AEF是等腰三角形时,m的值为
或
或
;
(3)连结PM,如图2,
∵BC与⊙P恰好相切于点M,
∴PM⊥BC,
∴PM∥AF,
而PA=PE,
∴PM为△EFA的中位线,
∴PM=
AF,
而PM=
AE,
∴AE=AF,
由(2)得当AF=AE,得m=
,
∴F点的坐标为(2,
).
 (1)∵正方形OABC的边长为2,M是BC的中点,
(1)∵正方形OABC的边长为2,M是BC的中点,∴CM=CM=1,CO∥AB,
∴∠CEM=∠F,
在△CEM和△BFM中
|
∴△CEM≌△BFM,
∴BF=CE,
∵E点坐标为(0,m),
∴CE=OC-OE=2-m,
∴BF=2-m,
∴AF=AB+BF=4-m,
∴F点坐标为(2,4-m)(0<m<2);
(2)AF2=(4-m)2,AE2=22+m2,EF2=22+(4-2m)2,
当AF=AE,则(4-m)2=22+m2,解得m=
| 3 |
| 2 |
当AF=EF,(4-m)2=22+(4-2m)2,整理得3m2-8m+4=0,解得m1=
| 2 |
| 3 |
当AE=EF,22+m2=22+(4-2m)2,整理得3m2-16m+16=0,解得m1=
| 4 |
| 3 |
综上所述,当△AEF是等腰三角形时,m的值为
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
(3)连结PM,如图2,
∵BC与⊙P恰好相切于点M,
∴PM⊥BC,
∴PM∥AF,
而PA=PE,
∴PM为△EFA的中位线,
∴PM=
| 1 |
| 2 |
而PM=
| 1 |
| 2 |
∴AE=AF,
由(2)得当AF=AE,得m=
| 3 |
| 2 |
∴F点的坐标为(2,
| 5 |
| 2 |
点评:本题考查了圆的综合题:掌握切线的性质定理、等腰三角形的性质和全等三角形的判定与性质;会利用两点间的距离公式计算线段的长;会利用因式分解法解一元二次方程;理解分类讨论的思想方法.

练习册系列答案
相关题目

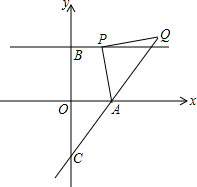 在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C. 有一数值转换器,原理如图,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是3,依次继续下去…,第2014次输出的结果是
有一数值转换器,原理如图,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是3,依次继续下去…,第2014次输出的结果是