题目内容
7. 如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE=$\sqrt{3}$.
如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE=$\sqrt{3}$.
分析 作CF⊥AD于F,由平行四边形的性质得出∠ADC=∠ABC=60°,CD=AB=4,OA=OC,求出∠DCF=30°,由直角三角形的性质得出DF=$\frac{1}{2}$CD=2,求出CF=$\sqrt{3}$DF=2$\sqrt{3}$,证出OE是△ACF的中位线,由三角形中位线定理得出OE的长即可.
解答 解:作CF⊥AD于F,如图所示: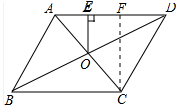
∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°,CD=AB=4,OA=OC,
∴∠DCF=30°,
∴DF=$\frac{1}{2}$CD=2,
∴CF=$\sqrt{3}$DF=2$\sqrt{3}$,
∵CF⊥AD,OE⊥AD,CF∥OE,
∵OA=OC,
∴OE是△ACF的中位线,
∴OE=$\frac{1}{2}$CF=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查了平行四边形的性质、直角三角形的性质、勾股定理、三角形中位线定理等知识;熟练掌握平行四边形的性质,证出OE是三角形的中位线是解决问题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.
在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.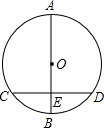 如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,若AB=6,则CD=3$\sqrt{3}$.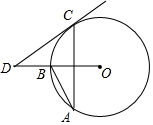 如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.
如图,AB、AC是⊙O的两条弦,∠A=30°,过点C的切线与OB的延长线交于点D,则∠D=30°.
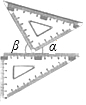 数学课上,小丽把一副三角板按如图所示的位置摆放(其中一个三角板的直角顶点在另一个三角板的直角边上),如果∠α=28°,那么∠β=62°.
数学课上,小丽把一副三角板按如图所示的位置摆放(其中一个三角板的直角顶点在另一个三角板的直角边上),如果∠α=28°,那么∠β=62°.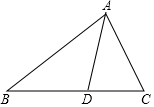 如图,AD是△ABC的角平分线,若AB:AC=5:3,则S△ABD:S△ACD=5:3,进而BC:CD=8:3.
如图,AD是△ABC的角平分线,若AB:AC=5:3,则S△ABD:S△ACD=5:3,进而BC:CD=8:3.