题目内容
17. 在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.
在△ABC中,AP为∠A的平分线,AM为BC边上的中线,过B作BH⊥AP于H,AM的延长线交BH于Q,求证:PQ∥AB.
分析 如图,延长BH交AC的延长线于E,延长AM,使得MN=AM.连接BN,CN.只要证明$\frac{AQ}{NQ}$=$\frac{PB}{PC}$,推出$\frac{MA+MQ}{AM-MQ}$=$\frac{BM+PM}{BM-PM}$,即$\frac{AM}{MQ}$=$\frac{BM}{PM}$,即可证明.
解答 解:如图,延长BH交AC的延长线于E,延长AM,使得MN=AM.连接BN,CN.
∵BM=CM,AM=MN,
∴四边形ABNC是平行四边形,
∴BN∥AE,BN=AC,
∴$\frac{BN}{AE}$=$\frac{NQ}{AQ}$,
∵∠BAH=∠EAH,AH⊥BE,
∴∠AHB=∠AHE=90°,
∴∠ABE+∠BAH=90°,∠E+∠EAH=90°,
∴∠E=∠ABE,
∴AB=AE,
∴$\frac{AB}{AC}$=$\frac{AQ}{NQ}$,
∵AP平分∠BAC,
∴$\frac{AB}{AC}$=$\frac{BP}{PC}$,
∴$\frac{AQ}{NQ}$=$\frac{PB}{PC}$,
∴$\frac{MA+MQ}{AM-MQ}$=$\frac{BM+PM}{BM-PM}$,
∴2AM•PM=2MQ•BM,
∴$\frac{AM}{MQ}$=$\frac{BM}{PM}$,
∴PQ∥AB.
点评 本题长相似三角形的判定和性质、平行线分线段成比例定理,角平分线的性质定理等知识,题目比较难,用到角平分线的性质定理,比例的性质.

练习册系列答案
相关题目
8. 如图所示,不含阴影部分的矩形(含正方形)的个数是( )
如图所示,不含阴影部分的矩形(含正方形)的个数是( )
 如图所示,不含阴影部分的矩形(含正方形)的个数是( )
如图所示,不含阴影部分的矩形(含正方形)的个数是( )| A. | 15 | B. | 24 | C. | 25 | D. | 26 |
 如图,架在消防车上的云梯AB的坡比为1:0.6.已知乙梯AB的长为16m,云梯底部离地面1.5m(即BC=1.5m),求乙梯顶端面的距离AE.
如图,架在消防车上的云梯AB的坡比为1:0.6.已知乙梯AB的长为16m,云梯底部离地面1.5m(即BC=1.5m),求乙梯顶端面的距离AE. 已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.
已知,如图,在四边形ABCD中,BC>BA,∠A+∠C=180°,DE⊥BC,BD平分∠ABC,试说明AD=DC.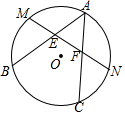 如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形.
如图所示,AB、AC是⊙O的两条弦.M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点,MN交AB、AC于点E、F.求证:△AEF是等腰三角形. 如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE=$\sqrt{3}$.
如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°,平行四边形ABCD的对角线AC、BD交于点O,过点O作OE⊥AD,则OE=$\sqrt{3}$.