题目内容
2．
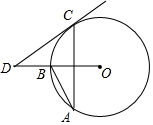如图，AB、AC是⊙O的两条弦，∠A=30°，过点C的切线与OB的延长线交于点D，则∠D=30°．
分析 连接OC，如图，根据切线的性质得∠OCD=90°，再根据圆周角定理得到∠BOC=2∠A=60°，然后利用互余计算∠D的度数．
解答 解：连接OC，如图，
∵CD为切线，
∴OC⊥CD，
∴∠OCD=90°，
∵∠BOC=2∠A=60°，
∴∠D=90°-∠COD=30°．
故答案为30．
点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
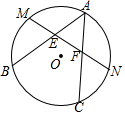如图所示，AB、AC是⊙O的两条弦．M、N分别是$\widehat{AB}$、$\widehat{AC}$的中点，MN交AB、AC于点E、F．求证：△AEF是等腰三角形．
已知：如图，在平行四边形ABCD 中，E为BC 中点，AE的延长线与DC的延长线相交于点F．求证：DC=CF．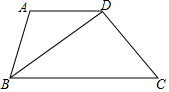
如图，在梯形ABCD中，AD∥BC，BD平分∠ABC，且CD⊥BD，若AD=5，BD=CD+2，则tan∠DBC=$\frac{3}{4}$．
如图，△ABC中AB=AC=13，BC=10，点D在边AB上，以D为圆心作⊙D，当⊙D恰好同时与边AC、BC相切时，此时⊙D的半径长为$\frac{120}{23}$．
如图，在平行四边形ABCD中，AB=4，BC=5，∠ABC=60°，平行四边形ABCD的对角线AC、BD交于点O，过点O作OE⊥AD，则OE=$\sqrt{3}$．