题目内容
已知关于x的方程mx2-3(m+1)x+2m+3=0.
(1)求证:无论m取任何实数,该方程总有实数根;
(2)若m≠0,抛物线y=mx2-3(m+1)x+2m+3与x轴的交点到原点的距离小于2,且交点的横坐标是整数,求m的整数值.
(1)求证:无论m取任何实数,该方程总有实数根;
(2)若m≠0,抛物线y=mx2-3(m+1)x+2m+3与x轴的交点到原点的距离小于2,且交点的横坐标是整数,求m的整数值.
考点:抛物线与x轴的交点,一元一次方程的解,根的判别式
专题:
分析:(1)由关于x的一元二次方程得到m不为0,根据方程有两个不相等的实数根,得到根的判别式大于0,列出关于m的不等式,求出不等式的解集即可得到m的范围;
(2)对于抛物线解析式,令y=0,表示出x,根据抛物线与x轴交点的横坐标都是整数,根据x的范围即可确定出m的整数值.
(2)对于抛物线解析式,令y=0,表示出x,根据抛物线与x轴交点的横坐标都是整数,根据x的范围即可确定出m的整数值.
解答:解:(1)由题意m≠0,
∵方程有两个不相等的实数根,
∴△>0,即[-3(m+1)]2-4m(2m+3)=(m+3)2>0,
解得:m≠-3,
则m的取值范围为m≠0和m≠-3;
(2)设y=0,则mx2-3(m+1)x+2m+3=0.
∵△=(m+3)2,
∴x=
,
∴x1=
,x2=1,
当x1=
是整数时,可得m=1或m=-1或m=3,
∵|x|<2,m=3不合题意舍去,
∴m的值为-1或1.
∵方程有两个不相等的实数根,
∴△>0,即[-3(m+1)]2-4m(2m+3)=(m+3)2>0,
解得:m≠-3,
则m的取值范围为m≠0和m≠-3;
(2)设y=0,则mx2-3(m+1)x+2m+3=0.
∵△=(m+3)2,
∴x=
| 3m+3±(m+3) |
| 2m |
∴x1=
| 2m+3 |
| m |
当x1=
| 2m+3 |
| m |
∵|x|<2,m=3不合题意舍去,
∴m的值为-1或1.
点评:此题考查了抛物线与x轴的交点,根的判别式,熟练掌握公式及法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
有4条线段长度分别为2cm,3cm,4cm,5cm,从中任意取三条线段能组成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
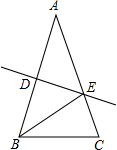 如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为点D,连接BE,如图AB=10,BC=3,则△EBC的周长为( )
如图,在△ABC中,AB=AC,AB的垂直平分线交AC于点E,垂足为点D,连接BE,如图AB=10,BC=3,则△EBC的周长为( )| A、10 | B、13 | C、16 | D、23 |
 已知直线y=
已知直线y=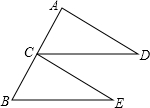 如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE.
如图,C是线段AB的中点,CD∥BE,且CD=BE,求证:AD=CE. 在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.
在如图所示的4×3网格中,每个小正方形的边长均为1,正方形顶点叫格点,连结两个网格格点的线段叫网格线段.点A固定在格点上.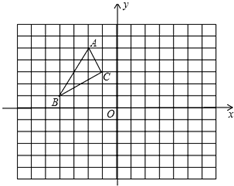 如图,△ABC的顶点坐标分别为A(-2,5)、B(-4,1)和C(-1,3).
如图,△ABC的顶点坐标分别为A(-2,5)、B(-4,1)和C(-1,3).