题目内容
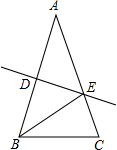如图，在△ABC中，AB=AC，AB的垂直平分线交AC于点E，垂足为点D，连接BE，如图AB=10，BC=3，则△EBC的周长为（ ）| A、10 | B、13 | C、16 | D、23 |
考点：线段垂直平分线的性质,等腰三角形的性质
专题：
分析：先根据线段垂直平分线的性质得出AE=BE，再根据AB=AC即可得出AC的长，进而得出结论．
解答：解：∵AB的垂直平分线交AC于点E，垂足为点D，
∴AE=BE，
∴BE+CE=AC，
∵AB=AC，AB=10，BC=3，
∴△EBC的周长=（BE+CE）+BC=AC+BC=10+3=13．
故选B．
∴AE=BE，
∴BE+CE=AC，
∵AB=AC，AB=10，BC=3，
∴△EBC的周长=（BE+CE）+BC=AC+BC=10+3=13．
故选B．
点评：本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．
练习册系列答案
相关题目
如图，有一张直角三角形的纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上且与AE重合，则BE的长为（ ）| A、2cm | B、3cm |
| C、4cm | D、5cm |
下列计算正确的是（ ）
A、-
| ||
B、（-
| ||
C、
| ||
D、-（-
|
若
是方程ax-y=3的解，则a的值（ ）
|
| A、1 | B、2 | C、4 | D、-5 |
使得多项式a2+b2-2ab-1的值为零的条件可写成（ ）
| A、a-b=±1 |
| B、a±b=1 |
| C、a+b=±1 |
| D、a±b=-1 |
如图，直线y=kx-2与x轴交于点A（1，0），与y轴交于点B，若直线AB上的点C在第三象限，且S△BOC=3，求点C的坐标．