题目内容
9.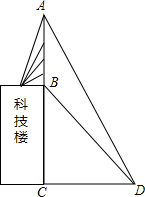 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
分析 在Rt△ACD中,根据CD的值可以求得AC的值,在Rt△BCD中,根据CD的值可以求得BC的值,根据AB=AC-BC即可求得AB的值,即可解题.
解答 解:在Rt△ACD中,AC=CD•tan60°=25×$\sqrt{3}$=25$\sqrt{3}$.
在Rt△BCD中,BC=CD•tan30°=$\frac{25\sqrt{3}}{3}$.
∴AB=AC-BC=25$\sqrt{3}$-$\frac{25\sqrt{3}}{3}$≈28.9(米).
答:该塔的高度约为28.9米.
点评 本题考查了特殊角的三角函数,考查了三角函数在直角三角形中的运用,本题中计算AC、BC的长是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
18. 某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )
某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )
 某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )
某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述不正确的是( )| A. | 抽样的学生共50人 | |
| B. | 50.5-60.5这一分数段的频率为0.08 | |
| C. | 估计优秀率(80分以上为优秀)在36%左右 | |
| D. | 60.5-70.5这一分数段的频数为12 |
 如图,在平面直角坐标系中,△ABC的位置如图所示.
如图,在平面直角坐标系中,△ABC的位置如图所示. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4. 如图,已知AD∥BC,P为CD上一点,且AP,BP分别平分∠BAD和∠ABC.
如图,已知AD∥BC,P为CD上一点,且AP,BP分别平分∠BAD和∠ABC.