题目内容
14. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点D在AC边上,将△ABD沿着直线BD翻折后,点A将在点E处,如果AD⊥DE,那么DE的长度为$4\sqrt{3}$-4.
分析 先根据题意画出图形,先依据含30°直角三角形的性质求得BC的长,然后依据勾股定理可求得CA的长,然后再求得∠CDB=45°,故此可得到△BCD为等腰直角三角形,则CD=4,最后依据DE=AD=AC-CD求解即可.
解答 解:如图所示.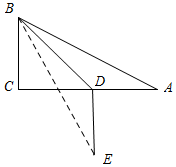
∵∠C=90°,∠A=30°,AB=8,
∴BC=4.
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4$\sqrt{3}$.
由翻折的性质可知∠ADB=∠EDB,DE=AD.
又∵AD⊥DE,
∴∠ADE=90°.
∴∠BDE=$\frac{1}{2}$×(360°-90°)=135°.
∴∠BDC=45°.
又∵∠BCD=90°,
∴BC=DC=4.
∴DE=AD=4$\sqrt{3}$-4.
故答案为:4$\sqrt{3}$-4.
点评 本题主要考查的是翻折的性质、勾股定理的应用,等腰直角三角形的判定,证得△BCD是等腰直角三角形是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
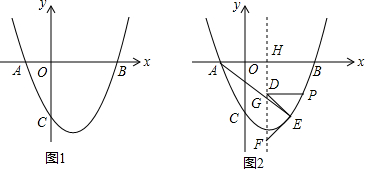 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC. 中,字母x的取值范围是( )
中,字母x的取值范围是( ) B.
B.  C.
C.  D.
D. 
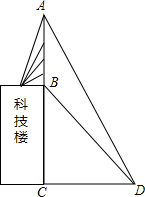 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)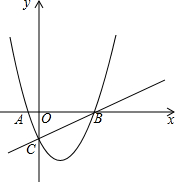 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数. 如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.
如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.