题目内容
18.(1)已知2x+3y-1=0,求9x•27y的值;(2)若x、y满足x+y=4,xy=2,求代数式x2+y2的值.
分析 (1)先将不同底数幂的两个数化为同底数幂,然后利用am•an=am+n.
(2)根据完全平方公式,可得(x2+y2)与(x+y)2的关系,从而求解.
解答 解:(1)∵由已知得:2x+3y=1,
∴9x•27y
=(32)x•(33)y
=32x•33y
=32x+3y
=31
=3;
(2)∵x+y=4,xy=2,
∴x2+y2
=(x+y)2-2xy
=16-2×2
=16-4
=12.
点评 本题考查了幂的乘方,同底数幂的乘法,完全平方公式,整式的混合运算和求值的应用,用了整体代入思想.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
7.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 直角三角形 | C. | 平行四边形 | D. | 菱形 |
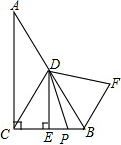 【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.
【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.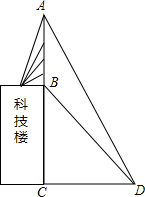 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米) 如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.
如图,将BM′绕点O按逆时针方向旋转45°后得到△A′OB′,若△AOB=15°,则∠AOB′的度数是30°.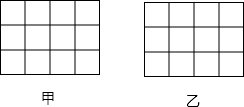 如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.