题目内容
3.当m=-$\frac{1}{2}$,分式$\frac{{m}^{2}}{{m}^{2}+2m+1}$÷(1-$\frac{1}{m+1}$)=-1.分析 首先计算括号内的式子,把分式的除法转化为乘法,进行约分即可化简,然后代入数值计算即可.
解答 解:原式=$\frac{{m}^{2}}{(m+1)^{2}}$÷$\frac{m}{m+1}$
=$\frac{{m}^{2}}{(m+1)^{2}}$•$\frac{m+1}{m}$
=$\frac{m}{m+1}$,
当m=-$\frac{1}{2}$时,原式=$\frac{-\frac{1}{2}}{-\frac{1}{2}+1}$=$\frac{-\frac{1}{2}}{\frac{1}{2}}$=-1.
故答案是:-1.
点评 本题考查了分式的混合运算,分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B.
B.  C.
C.  D.
D. 
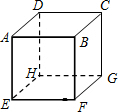 用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.
用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.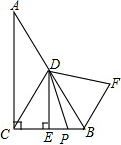 【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.
【探究】如图,在Rt△ABC中,∠ACB=90°,∠A=30°CD是AB边上的中线,DE⊥BC于E.P是线段CB上一点,连结DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连结BF,请猜想BC、BF、BP三者之间的数量关系,并证明你的结论.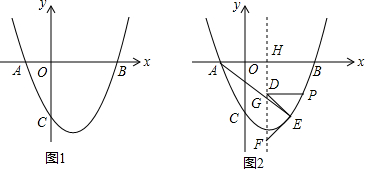 在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.
在平面直角坐标中,抛物线y=ax2-3ax-10a(a>0)分别交x轴于点A、B(点A在点B左侧),交y轴于点C,且OB=OC.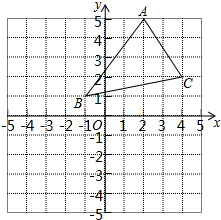 如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.
如图,在平面直角坐标系中,三角形ABC的三个顶点A、B、C的坐标分别为(-1,1),(4,2),(2,5),将三角形ABC向左平移3个单位长度,再向下平移5个单位长度.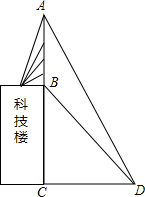 联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)
联通公司将移动信号收发塔建在某学校的科技楼上,李明同学利用测倾器在距离科技楼靠塔的一面25米处测得塔顶A的仰角为60°塔底B的仰角为30°,你能利用这些数据帮李明同学计算出该塔的高度吗?($\sqrt{3}$≈1.73,结果精确到0.1米)